Butterfly in Parabola
Experimental Mathematics

What Might This Be About?

Theorem

Let $P(0,y_{0})$ be a point on the axis of a parabola $y=x^{2}.$ Through $P$ two lines $AB$ and $CD$ are drawn, with $A,B,C,D$ on parabola. $AC$ and $BD$ cut the line $y=y_{0}$ at $M$ and $N,$ respectively.

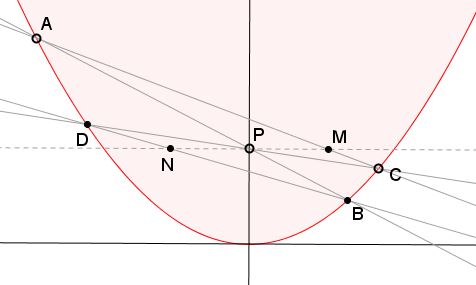
butterfly in parabola - problem

Then $PM=PN.$

The theorem is stated for the parabola $y=x^{2}$ but, since all parabolas are similar, it holds in the general case. The proof of the theorem depends on a lemma, see below.

Lemma

Given a parabola $y=x^{2}$ and three points $M(x_{0},y_{0}),$ $P(0,y_{0}),$ $N(-x_{0},y_{0}),$ $(y_{0}\gt 0, y_{0} \ne x_{0}^{2}).$ Line passing through $M$ intersects with the curve at $P_{1}(x_{1},y_{1})$ and $P_{2}(x_{2},y_{2});$ the extensions of $P_{1}P$ and $P_{2}P$ meet the curve at $P_{3}(x_{3}, y_{3})$ and $P_{4}(x_{4},y_{4}),$ respectively.

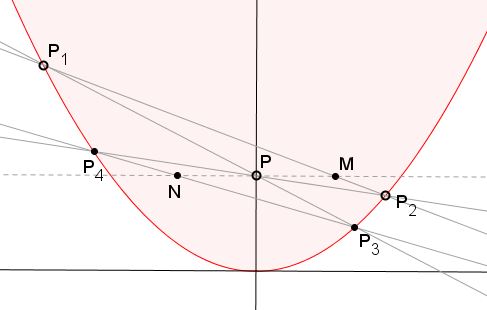
butterfly in parabola - lemma

Then $P_{3},$ $P_{4},$ and $N$ are collinear.

Proof of Lemma

Using the point-slope formula, we get the equation of $P_{1}P_{2}$:

(1)

$\displaystyle y=\frac{x_{2}^{2}-x_{1}^{2}}{x_{2}-x_{1}}(x-x_{1})+x_{1}^{2}=(x_{1}+x_{2})x-x_{1}x_{2}.$

Since $M$ is on $P_{1}P_{2}$ we have

(2)

$y_{0}=(x_{1}+x_{2})x_{0}-x_{1}x_{2}.$

The equation of $P_{1}P$ is, similarly, $\displaystyle y=\frac{x_{1}^{2}-y_{0}}{x_{1}}x+y_{0}.$ $P_{3}$ is the second intersection of $P_{1}P$ with the parabola, and can be found from $\displaystyle x^{2}=\frac{x_{1}^{2}-y_{0}}{x_{1}}x+y_{0},$ or

(3)

$x_{1}x^{2}-(x_{1}^{2}-y_{0})x-x_{1}y_{0}=0.$

The roots of (3) are the $x$-coordinates cf $P_{1}$ and $P_{3}$ so that $\displaystyle x_{1}+x_{3}= \frac{x_{1}^{2}-y_{0}}{x_{1}}$ and $x_{1}x_{3}=-y_{0}.$ So, $\displaystyle x_{3}=-\frac{y_{0}}{x_{1}}$ and $\displaystyle y_{3}=\big(\frac{y_{0}}{x_{1}}\big)^{2}.$ In a similar manner we get $\displaystyle x_{4}=-\frac{y_{0}}{x_{2}}$ and $\displaystyle y_{4}=\big(\frac{y_{0}}{x_{2}}\big)^{2}.$

The slope of $P_{3}P_{4}=m=\displaystyle\frac{y_{3}-y_{4}}{x_{3}-x_{4}}=-\frac{y_{0}(x_{1}+x_{2})}{x_{1}x_{2}}.$ Let $y=mx+b.$ Assuming it passes through $P_{4},$ yields $b=-\displaystyle\frac{y_{0}^{2}}{x_{1}x_{2}}.$ So, the equation of $P_{3}P_{4}$ is

(4)

$\displaystyle y=-\frac{y_{0}(x_{1}+x_{2})}{x_{1}x_{2}}x-\frac{y_{0}^{2}}{x_{1}x_{2}}.$

When $x=-x_{0}$ (4) yields $\displaystyle y=\frac{y_{0}}{x_{1}x_{2}}[x_{0}(x_{1}+x_{2})-y_{0}]=y_{0}$ (see (2)). Hence, $N$ lies on $P_{3}P_{4}$ and the three points $P_{3},$ $P_{4},$ $N$ are collinear.

Proof of Theorem

Let's denote $A=(x_{a},y_{a}),$ $B=(x_{b},y_{b}),$ $C=(x_{c},y_{c}),$ $D=(x_{d},y_{d}),$ $M=(p,y_{0}),$ $P=(0,y_{0}),$ $Q=(q,y_{0}).$

butterfly in parabola - problem

Let $y-y_{0}=k_{1}x$ and $y-y_{0}=k_{2}x$ be the equations of $AB$ and $CD,$ respectively. Since $A,$ $M,$ and $C$ are collinear,

$\displaystyle\frac{x_{a}-p}{x_{c}-p}=\frac{y_{a}-y_{0}}{y_{c}-y_{0}}=\frac{k_{1}x_{a}}{k_{2}x_{c}}.$

Solve this for $p$ to get

(5)

$\displaystyle p=\frac{(k_{1}-k_{2})x_{a}x_{c}}{k_{1}x_{a}-k_{2}x_{c}}.$

Similarly, since $B,$ $N,$ and $D$ are collinear,

(6)

$\displaystyle q=\frac{(k_{1}-k_{2})x_{b}x_{d}}{k_{1}x_{b}-k_{2}x_{d}}.$

Substituting the equation $y-y_{0}=k_{1}x$ of $AB$ into $y=x^{2}$ we have $x^{2}-k_{1}x-y_{0}=0,$ , whose roots are the $x$-coordinates of $A$ and $B,$ and $-y_{0}=x_{a}x_{b}$ and $k_{1}=x_{a}+x_{b}.$ So, $\displaystyle\frac{k_{1}x_{a}x_{b}}{x_{a}+x_{b}}=-y_{0}.$ Similarly, $\displaystyle\frac{k_{2}x_{c}x_{d}}{x_{c}+x_{d}}=-y_{0}.$ Equating the two gives

$k_{1}(x_{c}+x_{d})x_{a}x_{b}=k_{2}(x_{a}+x_{b})x_{c}x_{d}.$

This is equivalent to

$\displaystyle\frac{x_{a}x_{c}}{k_{1}x_{a}-k_{2}x_{c}}=-\frac{x_{b}x_{d}}{k_{1}x_{b}-k_{2}x_{d}}.$

By combining this result with (5) and (6) we see that $p=-q.$ Therefore, $PM=PN.$

Acknowledgment

The theorem and its proof are due to Sidney H. Kung.

Conic Sections > Parabola

Butterfly Theorem and Variants

71946940

Butterfly in Parabola Experimental Mathematics