Geometric Construction of Roots of Quadratic Equation

A quadratic equation

ax² + bx + c = 0,

with the leading coefficient a ≠ 0, has two roots that may be real - equal or different - or complex. The roots can be found from the quadratic formula:

x1,2 = (-b ± √b² - 4ac) / 2a,

(On a more extended discussion of solving and graphing the quadratic equation see the article Graph and Roots of Quadratic Polynomial.)

In addition to the four arithmetic operations, the formula includes a square root. This is exactly the kind of operations that produce constructible numbers from constructible numbers. (By being "constructible" we mean a length (of a straight line) segment that could be constructed by straightedge and compass, given a unit length.) In fact, Descartes used this example to introduce his ideas of analytic geometry.

I came across a generalization of Descartes' construction in an old translation (1910) of the classic The Theory of Geometric Constructions by August Adler (1863-1923).

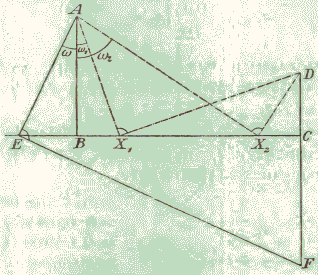
computing polynomials graphically

Following Adler, in order to solve the quadratic equation, form a broken right-angled line ABCD, with AB = a, BC = b, and CD = c taking account of the signs of the coefficients. For example, with c < 0, the segments AB and CD should be pointing in different directions:

computing polynomials graphically

Choose point E on BC and let ω be the ∠EAB. Introduce x = tan ω and find F on CD to make ∠AEF right. Then

BE = ax,
CE = ax + b,
CF = (ax + b)x,
DF = (ax + b)x + c.

It follows that DF = ax² + bx + c and, in case, F = D, x is naturally a solution to the quadratic equation ax² + bx + c = 0. The way to find a solution x is to locate point X on BC for which ∠AXD = 90°. How do you find such an X? Curiously, Adler suggest a neusis construction of sorts: use two rules attached at a right angle to make two perpendicular lines pass through A and D with a vertex on BC.

Except for the last part, the construction is immanently appealing. This is, of course, a graphical implementation of Horner's scheme and is easily extended to evaluating graphically polynomials of any degree greater than 1.

As to the solving of quadratic equations, the simple way of locating the required positions X with ∠AXD = 90°, is by drawing a circle on AD as diameter and finding where it intersects (if at all) the line BC. This is how it is done in the applet bellow. In the low left corner of the applet, there are three sliders each housing three points - yellow, red and blue (all draggable). The first two indicate the positions of 0 and 1 and thus the unit of measurement used by the slider. The distance of the blue dot to the yellow relative to the distance from the red one to the yellow, is given to the right of the slider. The sliders are numbered 0, 1, 2, corresponding to the coefficients a, b, c.

If you are reading this, your browser is not set to run Java applets. Try IE11 or Safari and declare the site https://www.cut-the-knot.org as trusted in the Java setup.

Geometric Construction of Roots of Quadratic Equation

What if applet does not run?

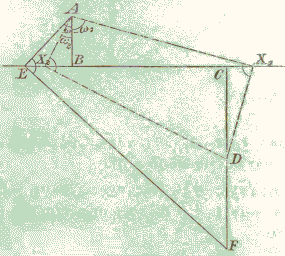
A slight inconsistency appears in Adler's diagram. Since x1 + x2 = -b, there is a confusion with signs. If BC, as depicted, is intended to correspond to a positive b, as is implied by the derivation of the length of DF, the two roots (in the case c is the same sign as a) can't be located on BC but should be rather on the other side of B. So, in the applet, to confirm to Adler's diagram I actually attempt to solve the equation ax² - bx + c = 0, swapping the sign of b.

Assuming X is between B and C and having BE = xa, consider similar triangles ABX and XCD. We have a proportion

x = ax / a = c / (b - ax)

from which

bx - ax² = c

or

ax² - bx + c = 0.

Alternatively, we can think of x and b (as probably Adler does) as having opposite positive directions. In this case, the sign minus in the latest quadratic equation is getting absorbed by x rather than b. (This has no effect on the value of x².)

Note

In 1867, when Adler was 4, l'Exposition Universelle was held in Paris; among a variety of exhibits there was a "machine" for determination of real roots of a polynomial created by an Austrian army captain Eduard Lill. Lill came up with an extension of the above method to polynomials of arbitrary degree. As Thomas C. Hull observes (Am Math Monthly, 118, April 2011, 307-315), Lill's method was still popular in the 1930. Nowadays it is much less so.


Quadratic Formula and Equation


|Activities| |Contact| |Front page| |Contents| |Algebra|

Copyright © 1996-2018 Alexander Bogomolny

72202151