Parabolic Reciprocity

What Might This Be About?

Problem

Given two parabolas $(V,UW)$ with the focus at $V$ and $UW$ as the directrix, and $(W,UV)$ with $W$ as the focus and $UV$ the directrix.

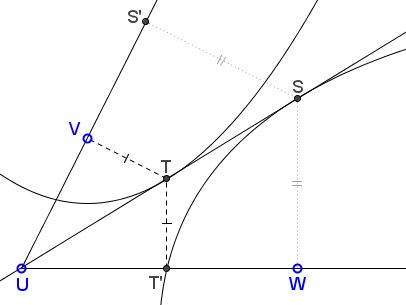
parabolic reciprocity, problem

Prove that the common tangent to the two parabolas passes through $U.$

Proof

Let $t$ be the tangent to $(V,UW)$ from $U$ and let $T$ be the point of tangency. Let $T'$ be the foot of the perpendicular from $T$ to $UW.$

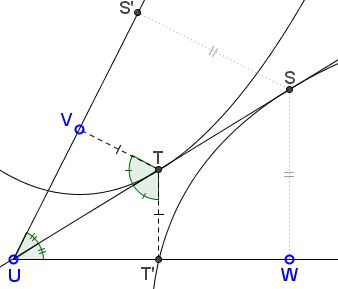
parabolic reciprocity, solution

By the tangent/bisector property, $\angle UTV=\angle UTT'.$ By the focal definition of parabola, $TV=TT'.$ It follows that $\Delta UTV=\Delta UTT',$ implying $\angle TUV=\angle TUT'.$ Thus $t$ is the angle bisector of $\angle VUW.$

The situation is absolutely symmetric with respect two the two parabolas, meaning that the tangent to $(W,UV)$ from $U$ also bisects $\angle VUW;$ thus, the two bisectors coincide.

Acknowledgment

The above statement is a lemma by Emmanuel José García posted at his blog site.

Conic Sections > Parabola

71536997