Parabolas Related to the Orthic Triangle
What Might This Be About?
Problem
Let $ABC$ be a triangle, with the orthic triangle $A'B'C'.$ Parabola with the focus at $A'$ and the directrix $B'C'$ is tangent to $AB,\;AC,\;BB',\;CC'.$
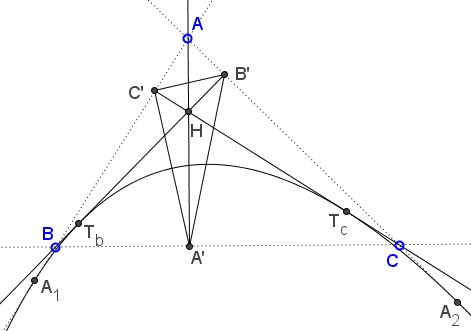
Proof
Due to the mirror property of the orthic triangle, $BB'$ is the bisector of $\angle A'B'C'.$ As been shown previously, the tangent to a parabola from a point on the directrix bisects the angle formed with the focus. Thus, $BB'$ is tangent to the parabola. And so does $CC'.$
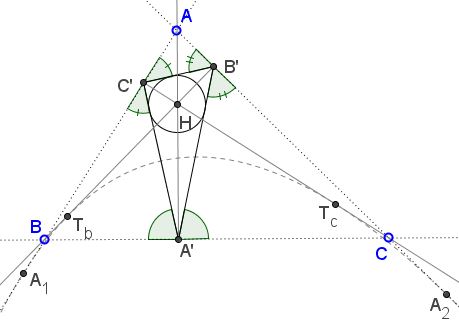
By the orthoptic property, two tangents to a parabola meet on the directrix if and only if they are perpendicular to each other. By the inverse, the line perpendicular to a tangent to a parabola at a point on the directrix is itself tangent to the parabola. Thus, since say $CC'$ is tangent to the parabola and $CC'\perp AB,$ i.e., $CC'\perp C'B,$ $C'B,$ i.e., $AB$ is also tangent to the parabola. The same holds for $BB'.$
Generalization
Quang Duong has commented on the CutTheKnotMath facebook page that the above is a special case of a more general problem:
Given a complete quadrilateral, with the Miquel point $M$ and the Steiner line (also known as the orthocentric line) $d$ then the parabola with focus $M$ and directrix $d$ is tangent to the $4$ sides of the complete quadrilateral.
Acknowledgment
A link to the above statement has been posted by Emmanuel José García at the CutTheKnotMath facebook page.
For the many properties of complete quadrilateral discovered by J. Steiner, see a 2004 article by Jean-Pierre Ehrmann Steiner's Theorems on the Complete Quadrilateral.
Quang Duong has commented on the CutTheKnotMath facebook page that the above is a special case of a more general problem:
Given a complete quadrilateral, with the Miquel point $M$ and the Steiner line (also known as the orthocentric line) $d$ then the parabola with focus $M$ and directrix $d$ is tangent to the $4$ sides of the complete quadrilateral.
A link to the above statement has been posted by Emmanuel José García at the CutTheKnotMath facebook page.
For the many properties of complete quadrilateral discovered by J. Steiner, see a 2004 article by Jean-Pierre Ehrmann Steiner's Theorems on the Complete Quadrilateral.
Conic Sections > Parabola
- The Parabola
- Archimedes Triangle and Squaring of Parabola
- Focal Definition of Parabola
- Focal Properties of Parabola
- Geometric Construction of Roots of Quadratic Equation
- Given Parabola, Find Axis
- Graph and Roots of Quadratic Polynomial
- Greg Markowsky's Problem for Parabola
- Parabola As Envelope of Straight Lines
- Generation of parabola via Apollonius' mesh
- Parabolic Mirror, Theory
- Parabolic Mirror, Illustration
- Three Parabola Tangents
- Three Points on a Parabola
- Two Tangents to Parabola
- Parabolic Sieve of Prime Numbers
- Parabolic Reciprocity
- Parabolas Related to the Orthic Triangle
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1966-2016 Alexander Bogomolny73599376
