Focal Definition of Parabola

Parabola is the locus of points equidistant from a given point (focus) and a given line (directrix).

Below is a dynamic illustration of the concept:

The ratio of the two distances is known as eccentricity, it applies to all conic sections; for parabola it is equal to $1.$ Parabola has an axis of symmetry which is perpendicular to the directrix and an vertex - midway between the focus and the directrix. It is customary to think - and this is justified in affine and projective geometries - that, as ellipse and hyperbola, parabola has two foci and two directrices but with one of each located at infinity.

Equation of Parabola in Cartesian Coordinates

Placing an vertex of the parabola at the origin, the focus at $(0,a)$ and the directrix at $y=-a,$ for some real $a,$ gives, for point $(x,y)$ on the parabola

$y+a = \sqrt{x^{2}+(y-a)^2},$

which, after squaring and simplifications, leads to $4ay=x^2.$ This accounts for $a$ both positive and negative; in the latter case, parabola is turned upside down. For parabola with a horizontal axis, the roles of $x$ and $y$ are reversed: $y^{2}=4ax.$

Equation of Parabola in Polar Coordinates

In polar coordinates $x=r\mbox{cos}\theta$ and $y=r\mbox{sin}\theta,$ where $r=\sqrt{x^2+y^2}$ is the distance to the origin, and $\theta$ is the angle between the $x-$axis and the vector from the origin to $(x,y).$ It is convenient to shift the parabola down as to place the focus at the origin:

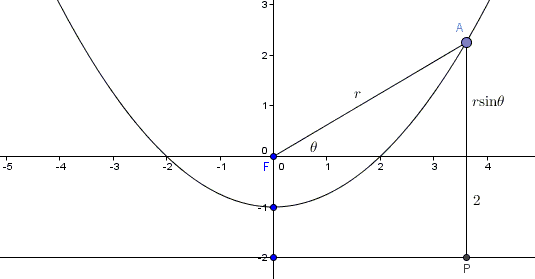
definition of parabola

The equations immediately simplifies to $r=r\mbox{sin}\theta+2a,$ or

$\displaystyle r=\frac{2a}{1-\mbox{sin}\theta}.$

For parabola with a horizontal axis the equation becomes $\displaystyle r=\frac{2a}{1-\mbox{cos}\theta}.$

References

D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
V. Gutenmacher, N. Vasilyev, Lines and Curves: A Practical Geometry Handbook , Birkhauser; 1 edition (July 23, 2004)
G. Salmon, Treatise on Conic Sections, Chelsea Pub, 6e, 1960
C. Zwikker, The Advanced Geometry of Plane Curves and Their Applications, Dover, 2005

Conic Sections > Parabola

72087683