Butterflies in a Pencil of Conics
What is this about?
Problem
Let $O$ be the midpoint of a given chord $RS$ of a proper (nondegenerate) conic $c_1,$ let two other chords $TU$ and $VW$ be drawn through $O,$ and let a conic $c_2$ through $T,$ $U,$ $V,$ $W$ cut the given chord in $E$ and $F.$
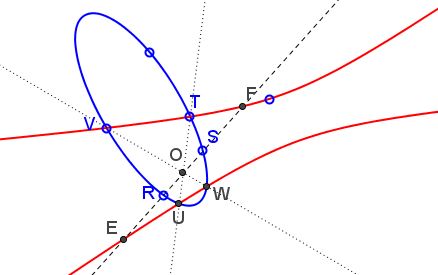
Then $O$ is the midpoint of $EF.$
Solution 1
Let $MN,$ the polar of $O$ for coinc $c_1,$ cut $TU$ in $M$ and $VW$ in $N.$
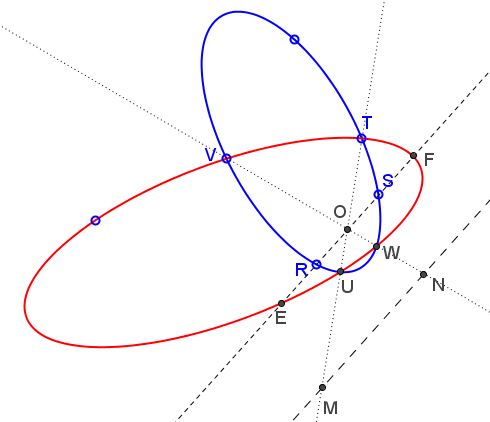
Then, since $(VWON)+(TUOM)=-1,$ $MN$ is also the polar of $O$ for conic $c_2.$ Moreover, $RS$ is parallel to $MN$ since $(RSO\infty )=-1.$ Therefore, $(EF)\infty )=-1$ and $O$ is the midpoint of $EF.$
(This is practically the same argument that was used in one of the proofs of the original Butterfly theorem.)
Solution 2
This solution is a straightforward adaptation of Hubert Shutrick's argument that was originally meant for the standard Butterfly theorem:
The pencil of conics that pass through $T,$ $U,$ $V,$ $W$ in the diagram include $c_1$ and the pair of lines $TU,$ $VW,$ whose intersection $O$ is a double point of the involution on $RS$ and the other double point must be the point at infinity since $M$ is the midpoint of $RS.$ Hence, it is also the midpoint of $EF$ because $c_2$ is another conic in the pencil.
References
- H. Eves, A Survey of Geometry, Allyn and Bacon, 1972
- D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988
Conics
- Conic Sections
- Conic Sections as Loci of Points
- Construction of Conics from Pascal's Theorem
- Cut the Cone
- Dynamic construction of ellipse and other curves
- Joachimsthal's Notations
- MacLaurin's Construction of Conics
- Newton's Construction of Conics
- Parallel Chords in Conics
- Theorem of Three Tangents to a Conic
- Three Parabolas with Common Directrix
- Butterflies in a Pencil of Conics
- Ellipse
- Parabola
- Butterfly theorem
- 2N-Wing Butterfly Theorem
- Better Butterfly Theorem
- Butterflies in Ellipse
- Butterflies in Hyperbola
- Butterflies in Quadrilaterals and Elsewhere
- Pinning Butterfly on Radical Axes
- Shearing Butterflies in Quadrilaterals
- The Plain Butterfly Theorem
- Two Butterflies Theorem
- Two Butterflies Theorem II
- Two Butterflies Theorem III
- Algebraic proof of the theorem of butterflies in quadrilaterals
- William Wallace's Proof of the Butterfly Theorem
- Butterfly theorem, a Projective Proof
- Areal Butterflies
- Butterflies in Similar Co-axial Conics
- Butterfly Trigonometry
- Butterfly in Kite
- Butterfly with Menelaus
- William Wallace's 1803 Statement of the Butterfly Theorem
- Butterfly in Inscriptible Quadrilateral
- Camouflaged Butterfly
- General Butterfly in Pictures
- Butterfly via Ceva
- Butterfly via the Scale Factor of the Wings
- Butterfly by Midline
- Stathis Koutras' Butterfly
- The Lepidoptera of the Circles
- The Lepidoptera of the Quadrilateral
- The Lepidoptera of the Quadrilateral II
- The Lepidoptera of the Triangle
- Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
- Two Butterfly Theorems by Sidney Kung
- Butterfly in Complex Numbers

Butterfly Theorem and Variants

|Contact| |Front page| |Contents| |Geometry| |Generalization|
Copyright © 1996-2018 Alexander Bogomolny
73564001
