Cross-Ratio

The cross-ratio is a surprising and a fundamental concept that plays a key role in projective geometry. In the spirit of duality, cross-ratio is defined for two sets of objects: 4 collinear points and 4 concurrent lines.

The cross-ratio (ABCD) of four collinear points A, B, C, D is defined as the "double ratio":

(1)	(ABCD) = CA/CB : DA/DB,

where all the segments are thought to be signed. The cross-ratio obviously does not depend on the selected direction of the line ABCD, but does depend on the relative position of the points and the order in which they are listed.

The cross-ratio (abcd) of four (coplanar and) concurrent lines is defined as another double ratio, now of sines:

(abcd) = sin(cMa)/sin(cMb) : sin(dMa)/sin(dMb),

where angles are also considered signed (in a natural way.) If points A, B, C, D are chosen on four lines a, b, c, d concurrent at M, then we often write (abcd) = M(ABCD). The fact that the four points (lines) are grouped into two pairs of points (lines) is reflected in another popular notation: (AB; CD) and (ab; cd).

The relationship between the two definitions is established by the following

Lemma

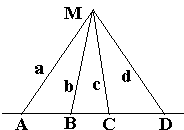
Let A, B, C, D be the points of intersection of 4 concurrent lines a, b, c, d by another straight line. Then (ABCD) = (abcd).

Remark

When the lines a, b, c, d are defined by the points, as above, it is often convenient to write (abcd) = M(ABCD).

Proof of Lemma

Consider 4 triangles CMA, CMB, DMA, and DMB and represent their areas in two different ways:

Area(CMA):	h·CA/2	= MC·MA·sin(CMA)/2
Area(CMB):	h·CB/2	= MC·MB·sin(CMB)/2
Area(DMA):	h·DA/2	= MD·MA·sin(DMA)/2
Area(DMB):	h·DB/2	= MD·MB·sin(DMB)/2,

where h is the length of the common altitude of the four triangles from vertex M. The required identity now follows immediately.

The lemma helps explain the significance of the cross-ratio in projective geometry.

Theorem 1

The cross-ratio of collinear points does not change under central (and, trivially, parallel) projections.

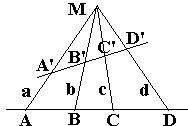
Indeed, from Lemma, (ABCD) = (abcd) = (A'B'C'D').

It's worth noting that central projection does not, in general, preserve either the distance or the ratio of two distances.

A permutation of the points may or may not change the cross-ratio. If any two pairs of points are swaped simultaneously, the cross-ratio does not change, e.g., (ABCD) = (BADC) = (DCBA). Wherever it changes, there are only five possible values. If (ABCD) = m, the possible values are 1-m, 1/m, (m-1)/m, 1/(1-m), m/(m-1).

If (ABCD) = 1, then either A = B or C = D. A more important case is where (ABCD) = -1. If (ABCD) = -1 then the points C and D are called harmonic conjugates of each other with respect to the pair A and B. A and B are then also harmonic conjugates with respect to C and D. Each of the pairs is said to divide the other's segment harmonically. There exists a straight edge only construction of harmonic conjugates. The four lines through an arbitrary point M and four conjugate points are called a harmonic bundle.

One of the four points may lie at infinity. On such occasions, it is useful to consider the limit when a finite point moves to infinity along the common line of the four. The limit is quite simple. For example, if D = , then (ABC) = CA/CB.

The theorem has been established by Pappus in the seventh book of his Mathematical Collections. It was further developed by Desargues starting with 1639 [Wells, p. 41].

As defined in (1), the cross ratio is meaningful for any four points not necessarily collinear. In this, more general form the cross-ratio is a useful concept, especially in inversive geometry, due to the following statement:

Theorem 2

The cross-ratio of any four coplanar points A, B, C, D is invariant under inversion:

(2)	(ABCD) = (A'B'C'D'),

where "primed" symbols are inverse images of their plain counterparts under any inversion whose center is different from any of the four given points.

Proof

Under an inversion with the coefficient k, we have:

C'A' = |k|·CA / (OC·OA),
C'B' = |k|·CB / (OC·OB),
D'A' = |k|·DA / (OD·OA),
D'B' = |k|·DB / (OD·OB),

which, upon completing the required operation and after some simplification, furnishes the proof.

References

J. N. Cederberg, A Course in Modern Geometries, Springer, 1995, Corrected third printing
R. Courant and H. Robbins, What is Mathematics?, Oxford University Press, 1996
D. Wells, The Penguin Dictionary of Curious and Intersting Geometry, Penguin Books, 1991

Cross-Ratio

40601162