Theorem of Three Tangents to a Conic

27 July 2014, Created with GeoGebra

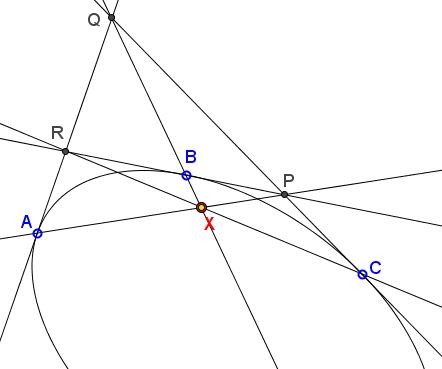
Then the three lines $AP,$ $BQ,$ $CR$ are concurrent at a point ($X$ in the above diagram.)

I had a chance to discuss and illustrate this theorem on several occasions: for a circle, for ellipse, as Gergonne's theorem, and in a related problem. It was observed that the theorem is of a projective nature and holds for every non-degenerate conic. Here I wish to emphasize that the projective character of the theorem goes even deeper, in the sense that in the projective space all non-degenerate conic are actually the same: there is no distinction between ellipses, parabolas, and hyperbolas.

Algebraically, projective space originates with the introduction of homogeneous coordinates and ideal elements. Starting with a two dimensional space $\mathbb{R}^{2}=\{(x,y):\,x,y\in\mathbb{R}\},$ we associate with any point pair $(x,y)$ an equivalence class of triples $(kx,ky,k,)$ $k\in\mathbb{R}^{*},$ i.e., $k$ is real and nonzero. As the next step, we consider equivalence classes of all triples $(x,y,z),$ where not all three coordinates are zero. Two triples $(x,y,z)$ and $(x',y',z')$ are considered equivalent if their (non-zero) coordinates are in the same ratio: $\displaystyle\frac{x}{x'}=\frac{y}{y'}=\frac{z}{z'},$ or are zero in corresponding pairs. Geometrically, such an equivalence class is identified with a straight line in $\mathbb{R}^{3}$ through the origin. This set has many notations; I'll be using $\mathbb{RP}^{2}.$

A straight line in $\mathbb{R}^2$ has an equation $ax+by+c=0,$ with $a$ and $b$ not both zero. Replacing $x=x'/z'$ and $y=y'/z'$ and multiplying by $z'$ gives $ax'+by'+cz'=0$ which is the equation of practically the same line in homogeneous coordinates. Indeed, it is almost the same. For, every point $(x,y)\in\mathbb{R}^2$ that satisfies $ax+by+c=0,$ its analogue $(kx,ky,k,)$ satisfies the homogeneous equation $ax'+by'+cz'=0.$ Conversely, if $(x',y',z')\in\mathbb{RP}^{2}$ satisfies $ax'+by'+cz'=0$ and $z'\ne 0,$ then $(x'/z',y'/z')$ satisfies $ax+by+c=0.$ The difference between the two lines - one in $\mathbb{R}^2$ the other in $\mathbb{RP}^2$ - is in the stipulation $z'\ne 0.$ For, the homogeneous equation $ax'+by'+cz'=0$ is easily seen to be satisfied by the equivalence class that contains the triple $(b,-a,0)!$ As a matter of fact, this point also lies the homogeneous image of every line parallel to $ax+by+c=0.$ But it does not belong to $\mathbb{R}^2$ and, for this reason, is known as an ideal element, or a point at infinity corresponding to the pencil of lines in $\mathbb{R}^2$ parallel to $ax+by+c=0.$ In particular it follows that in $\mathbb{RP}^2$ all lines intersect. The collection of points with the third coordinate $0$ is defined by the linear homogeneous equation $z=0$ and, thus, defines a line - an ideal line, or the line at infinity.

There may be a confusion: in the homogeneous coordinates, $z$ is no different from $x$ or $y,$ why then the equation $z=0$ defines a "line at infinity" whereas $x=0$ defines an ordinary line. The reason is this: the introduction of homogeneous coordinates allowed an extension - embedding - of $\mathbb{R}^2$ into $\mathbb{RP}^2$ by adding ideal elements - points and a line. However, $\mathbb{RP}^2$ while related to $\mathbb{R}^2,$ has a structure of its own. Within this structure there is no preferred line and the same holds for the points. Given $\mathbb{RP}^2,$ we may remove a line - any line - and obtain a structure equivalent to $\mathbb{RP}^2,$ for which the removed line would serve as a line at infinity. (Indeed, it won't automatically be an Euclidean space, but rather affine.) This simply means that the embedding $\mathbb{R}^2\subset\mathbb{RP}^2$ depends on the choice of the coordinate system in $\mathbb{R}^2.$ Removing a line from $\mathbb{RP}^2$ is known as specialization, and $\mathbb{R}^2$ is said to be a specialization of $\mathbb{RP}^2.$ Specialization can be achieved by removing any line in $\mathbb{RP}^2.$

With this preliminaries, let's consider what's happening to conics in passing from $\mathbb{R}^2$ to $\mathbb{RP}^2.$ A conic is defined by a second order equation. In $\mathbb{R}^2$ this is

$ax^{2}+by^{2}+dxy+ex+fy+c=0.$

The analogue of which in $\mathbb{RP}^2$ is

$ax^{2}+by^{2}+cz^{2}+dxy+exz+fyz=0$

that arise when we replace $x$ and $y$ with $x/z$ and $y/z.$ In $\mathbb{R}^2,$ there are distinct classes of conics, say, ellipses, parabolas, hyperbolas, each with its own characteristic properties - some similar but many distinct. (E.g., ellipses are bounded, hyperbolas have asymptotes, all parabolas are similar.) That is not the case in $\mathbb{RP}^2.$

As an example, consider the equation $x^{2}-yz=0$ and different specializations of $\mathbb{RP}^2.$ If we choose $x=0$ as the ideal line at infinity, the equation reduces to $yz=1$ (with the intermediate step $\displaystyle 1-\frac{y}{x}\frac{z}{x}=0.)$ This equation describes a hyperbola in $\mathbb{R}^2.$ If $y=0$ is taken to be the ideal element, the equation reduces to first $\displaystyle\bigg(\frac{x}{y}\bigg)^{2}-\frac{z}{y}=0$ and then to $x^{2}=z$ which is a parabola in $\mathbb{R}^2.$ Finally, let's choose $y+z=0$ as the line at infinity. To see what happens, let's make a substitution $y=y'+z',$ $z=y'-z':$ $x^{2}-(y')^{2}+(z')^{2}=0.$ Drop now the apostrophe and choose $y=0$ as the ideal line: $\displaystyle\bigg(\frac{x}{y}\bigg)^{2}-1+\bigg(\frac{z}{y}\bigg)^{2}=0,$ or, in $\mathbb{R}^2,$ $x^{2}+z^{2}=1,$ a circle.

Note that collinearity, concurrence, tangency are preserved in embedding of $\mathbb{R}^2$ into $\mathbb{RP}^2$ and the converse specialization (although, this begs for a more detailed treatment). This is why, say, the validity of the three tangents theorem for circles implies its validity for all non-degenerate conics.

1. D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
2. D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988
3. C. R. Wylie, Jr., Introduction to Projective Geometry, Dover, 1970