Three Parabolas with Common Directrix

What is this about?

Problem

If three parabolas share a common directrix and each pair intersect each other in two points, then, the lines joining the two intersection points of each pair of parabolas are concurrent.

More accurately, assume parabolas $c,$ $d,$ and $e,$ with foci $C,$ $D,$ and $E,$ respectively, share the directrix $s.$ Assume also that $c\cap d=\{H,J\},$ $c\cap e=\{I,K\},$ and $d\cap e=\{F,G\}.$

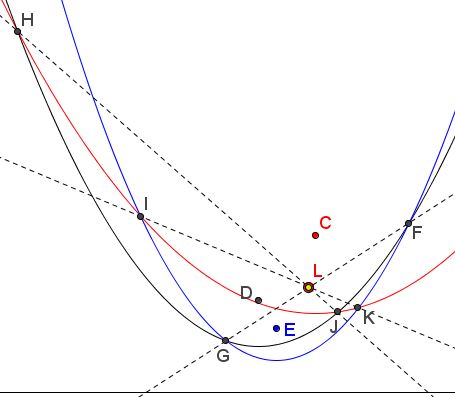
Three Parabolas with Common Directrix - problem

Then common chords $FG,$ $HJ,$ and $IK,$ are concurrent.

Proof

Parabola is the locus of points equidistant from a given point (focus) and a given line (directrix). If $\rho (X,Y)$ denotes the distance between two objects $X$ and $Y$ then

$\begin{align} \rho (C,K)=\rho (K,s)=\rho (E,K)\\ \rho (C,I)=\rho (I,s)=\rho (E,I), \end{align}$

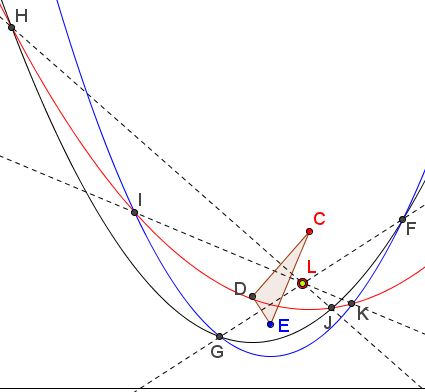
implying that $IK$ is the perpendicular bisector of $CE.$ Similarly, $JH$ is the perpendicular bisector of $CD$ and $FG$ is that of $DE.$ It follows that the three lines meet at the circumcenter of $\Delta CDE.$

Three Parabolas with Common Directrix - solution

Elliptic Analogy

The common directrix played such an important role in the proof of the statement about parabolas that it begged for an immediate generalization, viz., the statement is true for any three conics with the same eccentricity that share a directrix, for example, three ellipses or three hyperbolas. (Perhaps, for a generalization, caution needs to be exercised as regard the existence or the choice of the common points, and, hence chords, but he proof would remain exactly the same.)

However, there is an analogous statement about ellipses that does not mention directrices (Ilya I. Bogdanov, Two theorems on the focus-sharing ellipses: a three-dimensional view), the proof, though, does.

Let $E_1,$ $E_2,$ $E_3$ be three ellipses such that each two of them share a common focus. We assume that none of the ellipses lies inside the other one. Note that there exist two different configurations satisfying this property: three ellipses with a common focus, and three ellipses with the pairs of foci $(A, B),$ $(A, C),$ and $(B, C).$

Let $Aij,$ $Bij$ $(1 = i \lt j = 3)$ be the points of intersection of ellipses $E_i$ and $E_j.$ Then the lines $A_{12}B_{12},$ $A_{13}B_{13},$ and $A_{23}B_{23}$ are concurrent.

Three Ellipses with Common foci - an illustration

Conic Generalization

If three conics have two common points (which may coincide or be imaginary) then the lines joining the other two intersections of each pair of the conics are concurrent.

Proof:

In this case three parabolas have two common points at infinity. Project these two common points into circular points (meaning project the parabolas into circles); apply the radical center theorem; arrive at the conclusion.

(A short explanation on the meaning of circular points can be found in Hubert Shutrick's article.)

Acknowledgment

The original problem was proposed by Emmanuel Antonio José García (Dominican Republic). The proof is by Luis González. The statement on the conics and its proof are due to Telv Cohl. The reference to Ilya Bogdanov's paper has been supplied by Antonio García whom, together with Telv Cohl, I owe my sincerest thanks.

Conics

72260793