Nobbs' Points, Gergonne Line

Nobbs' Points, Gergonne Line
What are they?
A Mathematical Droodle

Nobbs' Points, Gergonne Line

The applet attempts to illustrate the following theorem:

Assume A', B', C' are the points of contact of the incircle of ΔABC: A' on side BC, etc. Denote the intersection of AB and A'B' as C'', that of AC and A'C' as B'', and let A'' be the intersection of BC and B'C'. Then points A'', B'', and C'' are collinear.

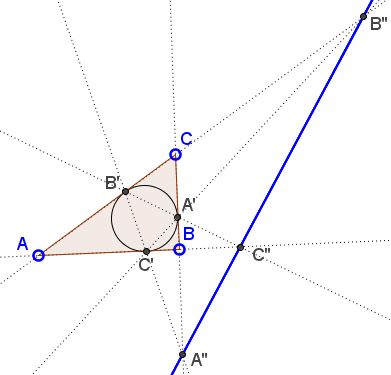
Gergonne line

The points A'', B'', and C'' are known as Nobbs' points. The theorem tells us the Nobbs' points of a triangle are collinear. The line the points lie on was named the Gergonne line by Adrian Oldknow [Oldknow, pp. 324-325] after J. D. Gergonne. The reason for the name is as follows.

It is known that the lines AA', BB', and CC' meet at the Gergonne point Ge of ΔABC. Put another way, this means that two triangles ABC and A'B'C' are perspective in Ge. By Desargues' theorem, triangles perspective from a point are also perspective from a line. Thus the corresponding side lines of triangles ABC and A'B'C' cross in the points that belong to the same line. This is the Gergonne line of Oldknow.

I'll give an additional argument in support of that nomenclature: the Gergonne line is the polar of the Gergonne point Ge in the incircle of ΔABC. Indeed,

A'B' is the polar of C,

AB is the polar of C'. Therefore,

C'' is the pole of CC', by La Hire's theorem.

Similarly, A'' is the pole of AA' and B'' is the pole of BB'. Since their polars AA', BB', and CC' are concurrent (in the Gergonne point Ge), the poles A'', B'', and C'' are collinear to a line (the Gergonne line, naturally.)

Note that if one of the triangles ABC and A'B'C' is equilateral, so is the other, and in this case the Gergonne line is the line at infinity.

Remark

ΔA'B'C' is known as the contact triangle (and also Gergonne triangle) of ΔABC. ΔABC is the tangent(ial) triangle of ΔA'B'C'.

(From a somewhat different perspective this same configuration is studied elsewhere. A more general statement is also available.)

References

A. Oldknow, The Euler-Gergonne-Soddy Triangle of a Triangle, Amer Math Monthly, Vol. 103, No. 4 (Apr. 1996), 319-329

Poles and Polars

Symmedian

Desargues' Theorem

71925244

A'B'	is the polar of	C,
AB	is the polar of	C'.	Therefore,
C''	is the pole of	CC',	by La Hire's theorem.