6 to 9 Point Circle: What Is This About?
A Mathematical Droodle

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2012 Alexander Bogomolny

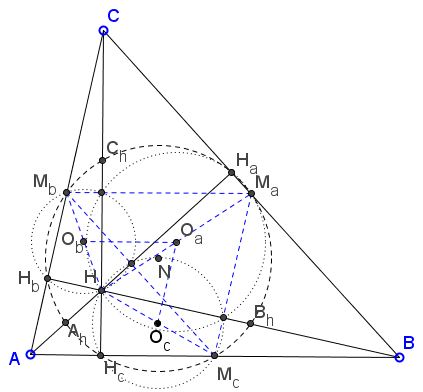
Bui Quang Tuan came up with a novel proof based on the recent theorem of six concyclic points. Let, as usual, H denote the orthocenter of ΔABC. The proof begins with a construction of three circles (O_a), (O_b), (O_c), which are the circumcircles of triangles HH_aM_a, HH_bM_b, HH_cM_c. Of course the three centers O_a, O_b, O_c are the midpoints of HM_a, HM_b, HM_c. Two circles (O_b), (O_c) share one common point at H. Their other common point is the reflection of H in O_bO_c therefore it is on altitude AH_a. (This is because O_bO_c ⊥ HH_a.) Similarly we can show: three circles (O_a), (O_b), (O_c) share one common point at H and another common points are one Cevians (altitudes) AH_a, BH_b, CH_c. By the six concyclic points theorem, H_a, H_b, H_c, M_a, M_b, M_c are concyclic on a circle, say, (N). In words,

Applying this statement to, say, ΔCAH we see that its circle (N) passes through the midpoints of its sides, viz., C_h, A_h, M_b and, of course, through the feet of the altitudes, which happen to be H_a, H_b, H_c. The circles (N) formed for triangles ABH also BCH, also pass through H_a, H_b, H_c so that all three coincide. The latter two pass through A_h, B_h, M_c and B_h, C_h, M_a, respectively. It follows that the common (N) circle passes through all the nine points.

Nine Point Circle

• Nine Point Circle: an Elementary Proof
• Feuerbach's Theorem
• Feuerbach's Theorem: a Proof
• Four 9-Point Circles in a Quadrilateral
• Four Triangles, One Circle
• Hart Circle
• Incidence in Feuerbach's Theorem
• Six Point Circle
• Nine Point Circle
• 6 to 9 Point Circle
  • Six Concyclic Points
• Six Concyclic Points II
• Bevan's Point and Theorem

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2012 Alexander Bogomolny