The circumcircle of a triangle formed by two vertices and the orthocenter of a given triangle is equal to the circumcircle of the given triangle.
The circumcircle of a triangle formed by two vertices and the orthocenter of a given triangle is equal to the circumcircle of the given triangle.
Solution
One solution is based on a property of the orthocenter: its reflection in a side of the triangle falls on the circumcenter. In other words, the segment of an altitude extended between the orthocenter and the second intersection with the circumcircle is bisected by the corresponding side of the triangle.
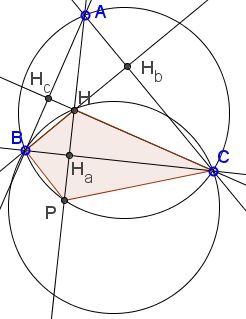
Let ΔABC be given. H is the orthocenter and Ha the foot of the altitude from A (Hb and Hc are defined likewise.) Let AHa cross the circumcircle the second time in, say, P. Then HHa = PHa, giving ΔHBC = ΔPBC. If two triangles are equal. so are their circumcircles. But the circumcircle of ΔPBC coincides with that of ΔABC thus proving the statement.
Douglas Rogers reports that the problem in a little different guise but with a superbly different solution has been posed in the Mathematical Repository (New Series) published by Thomas Leybourn (Question 377). Two solutions appeared in volume IV (1819), 91-92. Of these the second solution by the proposer (Mr. Cunliffe) was essentially as above. But the first one, by a mysterious Lady, was essentially different. The applet illustrates that solution. But first the problem as it appeared in the Mathematical Repository:
What is the relation of the diameters of the three circles, passing through the extremities of the sides, and point of intersection of the perpendiculars from the angles upon the sides of a plane triangle?
The answer is of course that all three are equal and, moreover, they are equal to the circumdiameter of the given plane triangle.
Let HA', HB', HC' be diameters of the three circles. Since ∠HBA' is subtended by a diameter in circle BCH, ∠HBA' = 90°. Similarly ∠HBC' = 90°. It follows that A'BC' is a straight line. Similarly, C'AB' and B'CA' are straight.
One may make an additional observation. HC the orthogonal bisector of side A'B', HB and HA are the orthogonal bisectors of sides A'C' and B'C'. So, A'C = B'C, and so on, and we see that all four triangles ABC, A'BC, AB'C, and ABC' are equal. So that not only "the ratio of the diameters (in question) is that of equality" but the three are indeed equal to the circumdiameter of ΔABC. ΔA'B'C' is the anticomplementary triangle of ΔABC, with H as its circumcenter.
Douglas Rogers has informed me that the mysterious Lady in question was none other than Mary Fairfax Somerville (1780--1872), a translator of Laplace's Mécanique Céleste, among many other achievements.
