Bevan's Point and Theorem
What is it?
A Mathematical Droodle
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
The applet attempts to suggest a problem proposed by Benjamin Bevan (1804) and solved by John Butterworth the same year. Let V be the circumcenter of the excentral triangle IaIbIc of ΔABC. Let I and O be the incenter and the circumcenter of ΔABC. Then
- I, O, V are collinear and IO = OV, and
- The circumradius of ΔIaIbIc is twice the circumradius of ΔABC.
The configuration has additional properties. For example,
- the lines joining V with the excenters are perpendicular to the respective sides of ΔABC,
- I and V are equidistant from the Euler line of ΔABC,
- the circumcircle of ΔABC serves as the nine-point circle of ΔIaIbIc.
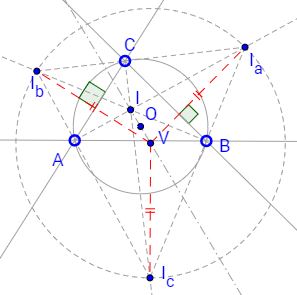
Point V is known as the Bevan point of ΔABC and the circumcircle of its excentral triangle is often referred to as the
An important observation that explains many properties of the excentral triangle is that the reference ΔABC is the orthic triangle of its excentral ΔIaIbIc. This is so because the excentral triangle is formed by the external angle bisectors of the reference triangle which are perpendicular to its internal angle bisectors. An immediate implication is that, due to the uniqueness of the triangle possessing the mirror property, the incenter I of ΔABC serves as the orthocenter of ΔIaIbIc.
This observation actually proves 1-5 all at once. The circumcircle of ΔABC passes through the feet of altitudes in ΔIaIbIc meaning that it's the nine-point circle in that triangle and proving #5. Its center (C), therefore, is midway between its circumcenter (V) and the orthocenter (I) proving #1. In any triangle, the radius of the nine-pointer circle is half that of the circumcircle proving #2.
#3 is the consequence of the fact that, in any triangle, the lines joining a vertex to the orthocenter and the circumcenter are isogonal conjugate. Any two points are equidistant from any line that passes through their midpoint, which proves #4 since the circumcenter O is on the Euler line of ΔABC.
The configuration of a reference and its excentral triangles conceals many more curiosities. Some of these are discussed elsewhere.
Nine Point Circle
- Nine Point Circle: an Elementary Proof
- Feuerbach's Theorem
- Feuerbach's Theorem: a Proof
- Four 9-Point Circles in a Quadrilateral
- Four Triangles, One Circle
- Hart Circle
- Incidence in Feuerbach's Theorem
- Six Point Circle
- Nine Point Circle
- 6 to 9 Point Circle
- Six Concyclic Points II
- Bevan's Point and Theorem
- Another Property of the 9-Point Circle
- Concurrence of Ten Nine-Point Circles
- Garcia-Feuerbach Collinearity
- Nine Point Center in Square
References
- R. A. Johnson, Advanced Euclidean Geometry (Modern Geometry), Dover, 2007, p. 197
- D. Wells, Curious and Interesting Geometry, Penguin Books, 1991
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73580992
