Nine Point Circle: What Is This About?
A Mathematical Droodle

Explanation

The applet purports to suggest a proof for the existence of the 9-point circle. The proof was brought to my attention by Hubert Shutrick. Here is the statement of existence:

In ABC, the midpoints of the sides MA, MB, MC, the feet HA, HB, HC of the altitudes, and the midpoints AH, BH, CH of the segments connecting the orthocenter with the vertices, lie on a circle, known as the 9 point circle.

The proof is illustrated by the applet:

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

Buy this applet What if applet does not run?

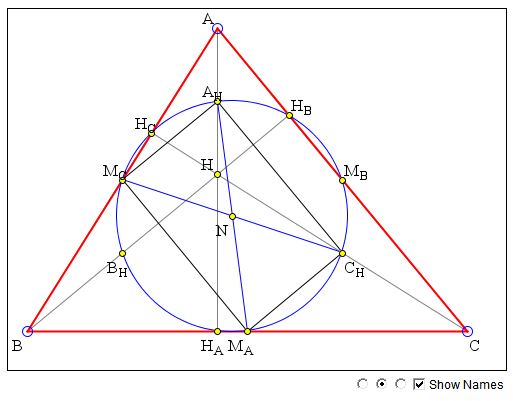
First of all, M_BM_C is the midline in ΔABC so that it's parallel to BC and equals half of the latter. The same holds of B_HC_H which is a midline in ΔHBC. It follows that M_BM_CB_HC_H is a parallelogram. But more is true. M_BC_H is a midline in ΔAHC. In particular, this implies that M_BC_H is orthogonal to BC (as it is parallel to AH.) Hence the quadrilateral M_BM_CB_HC_H is a rectangle.

Observe that the diagonals of a rectangle (of a parallelogram in fact) cross at their midpoints. Let N be the center of the rectangle M_BM_CB_HC_H.

Rectangles M_CM_AC_HA_H and M_AM_BA_HB_H are obtained in a similar way. Between them, the three rectangles share three diagonals: M_AA_H, M_BB_H, M_CC_H and therefore have a common center. This shows that 6 points - M_A, M_B, M_C, A_H, B_H, C_H lie on a circle with center N.

Furthermore, in ΔA_HH_AM_A the angle at H_A is right whereas the hypotenuse A_HM_A serves as a diameter of the just found circle. It follows that H_A also lies on that circle, and similar argument applies to the feet of the remaining altitudes, H_B and H_C.

Nine Point Circle

• Feuerbach's Theorem
• Feuerbach's Theorem: a Proof
• Four 9-Point Circles in a Quadrilateral
• Four Triangles, One Circle
• Hart Circle
• Incidence in Feuerbach's Theorem
• Six Point Circle
• Nine Point Circle
• 6 to 9 Point Circle
  • Six Concyclic Points
• Six Concyclic Points II
• Bevan's Point and Theorem