Concurrence of Ten Nine-Point Circles
What Might This Be About?
Problem
Given point $P$ in the plane of $\Delta ABC,$ let $H$ be the orthocenter of the triangles; consider three quadrilaterals $ABPH,$ $BCPH,$ and $ACPH.$ Each quadrilateral defines four triangles whose nine-point circles concur at a point, known as the Euler-Poncelet points of the quadrilateral.
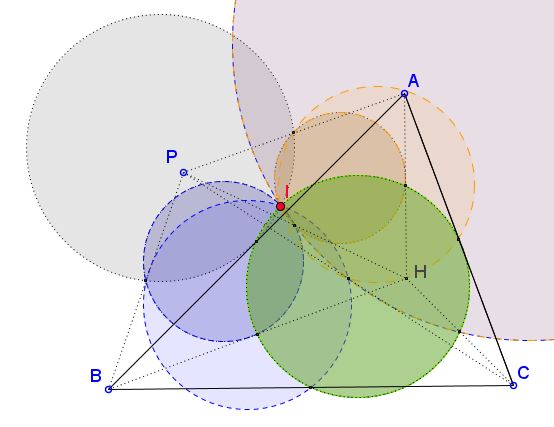
Prove that the three Euler-Poncelet points coincide.
Solution
Solution is wanting; meanwhile you may wonder why the caption says "10 circles" instead of $4\times 3=12.$
Also, it has been observed that, similar to Griffiths' theorem, that point is the same for all points $P$ on a straight line through the circumcenter of $\Delta ABC.$
Acknowledgment
The problem has been posted by Dao Thanh Oai at the CutTheKnotMath facebook page.
Nine Point Circle
- Nine Point Circle: an Elementary Proof
- Feuerbach's Theorem
- Feuerbach's Theorem: a Proof
- Four 9-Point Circles in a Quadrilateral
- Four Triangles, One Circle
- Hart Circle
- Incidence in Feuerbach's Theorem
- Six Point Circle
- Nine Point Circle
- 6 to 9 Point Circle
- Six Concyclic Points II
- Bevan's Point and Theorem
- Another Property of the 9-Point Circle
- Concurrence of Ten Nine-Point Circles
- Garcia-Feuerbach Collinearity
- Nine Point Center in Square
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73569008
