Feuerbach's Theorem: What Is It About?
A Mathematical Droodle
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
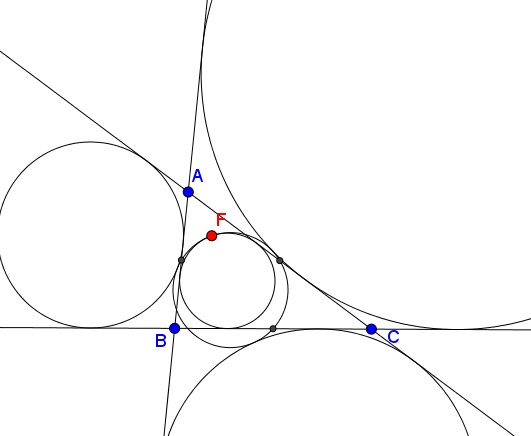
This is a famous result discovered by Karl Wilhelm Feuerbach (1800-1834): the 9-point circle of a triangle touches its incircle and the three excircles. Feuerbach proved the theorem by computing algebraically the distances between the centers of the circles. Other proofs depend on the inversion in a circle. The point of tangency of the incircle and the 9-point circle is known as the Feuerbach point. The 9-point circle is known to house a few dozen other intereseting points. The points of tangency in Feuerbach's theorem are involved in two cases of incidence.
Nine Point Circle
- Nine Point Circle: an Elementary Proof
- Feuerbach's Theorem
- Feuerbach's Theorem: a Proof
- Four 9-Point Circles in a Quadrilateral
- Four Triangles, One Circle
- Hart Circle
- Incidence in Feuerbach's Theorem
- Six Point Circle
- Nine Point Circle
- 6 to 9 Point Circle
- Six Concyclic Points II
- Bevan's Point and Theorem
- Another Property of the 9-Point Circle
- Concurrence of Ten Nine-Point Circles
- Garcia-Feuerbach Collinearity
- Nine Point Center in Square
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73558848
