Nine Point Center in Square
Problem
Lemma
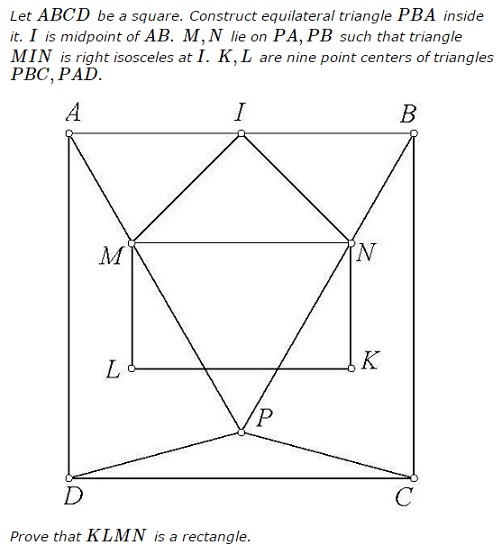
In a $75-30-75\,$ isosceles triangle, the nine point center forms a right isosceles triangle with the base:
Proof of Lemma
Let us choose an orthogonal coordinate system with $X\,$ axis pointing to the right and $Y\,$ axis pointing from point $O\,$ to point to $B.\,$ Let $G\,$ denotes the centroid of $\Delta PBC.\,$ And let $\hat{x}\,$ and $\hat{y}\,$ be the unit vectors along the axes; $L=OK,\,$ $R\,$ the circumradius of $\Delta PBC.\,$ $\displaystyle\overrightarrow{OG}=\frac{1}{3}(\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OP})=-R\left(\frac{\sqrt{3}-1}{3}\right)\hat{y}.\,$ From a property of the nine-point center, $KO=3\cdot KG.\,$ In our case, this is equivalent to $\displaystyle OG=\frac{2}{3}OK.\,$ Thus $\displaystyle R\left(\frac{\sqrt{3}-1}{3}\right)=\frac{2L}{3},\,$ or $\displaystyle L= R\left(\frac{\sqrt{3}-1}{2}\right).\,$ If we prove that $\angle CKP=90^{\circ},\,$ then by symmetry, the other two angles of the triangle will be $45^{\circ},\,$ proving $\Delta CKP\,$ is $45-90-45.\,$
Taking the scalar product,
$\displaystyle\begin{align} \overrightarrow{CK}\cdot\overrightarrow{PK} &=\left[-\frac{R}{2}\hat{x}-\left(L-R\frac{\sqrt{3}}{2}\right)\hat{y}\right]\cdot\left[\frac{R}{2}\hat{x}-\left(L-R\frac{\sqrt{3}}{2}\right)\hat{y}\right]\\ &=\left[-\frac{R}{2}\hat{x}+\frac{R}{2}\hat{y}\right]\cdot\left[\frac{R}{2}\hat{x}+\frac{R}{2}\hat{y}\right]\\ &=0. \end{align}$
Thus, $\angle CKP=90^{\circ}.$
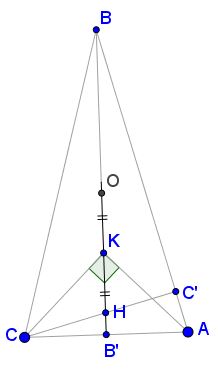
Solution 1
Draw right isosceles triangle $CKP\,$ and circle $(KMP).$
We now recourse to angle chasing.
$\begin{align} \angle KPM &= 360^{\circ}-\angle APD-\angle CPD-\angle CPK\\ &=360^{\circ}-75^{\circ}-150^{\circ}-45^{\circ}\\ &=90^{\circ}, \end{align}$
making $KM\,$ a diameter of $(KMP).\,$ Let $O\,$ be the second intersection of the circle with $BB',\,$ the axis of the isosceles $\Delta CBP.\,$ Then, too, $\angle KOM=90^{\circ},\,$ i.e., $OM\perp BB'.\,$
Let $N'\,$ be the second intersection of $(KMP)\,$ and $BP.\,$ $\angle KN'M=90^{\circ}.$
$\angle KMN'=\angle KPN' = \angle KPM-\angle BPM=30^{\circ}.$
Hence $\angle MN'P=60^{\circ}.\,$ If $S=MK\cap BC,\,$ then $\angle MSB=60^{\circ}\,$ because $KM\perp BP.\,$ It follows that $KN'\parallel BC\,$ and, subsequently, $MN'\parallel AB,\,$ implying $N'=N.$
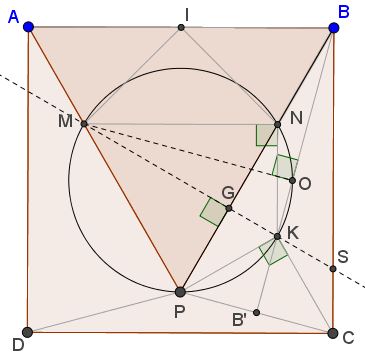
Extras
The configuration has many more features that are not difficult to verify.
- $KP=KC=KN=BN.$
- $KS=CS.$
- $O\,$ is the circumcenter of $\Delta BCP.$
- $\Delta COP\,$ is equilateral.
- $MP\,$ is the bisector of $\angle KMN.$
Properties of $\Delta BCP,\,$ a $75-30-75\,$ triangle, have played above (and will play below) an important role, naturally. Further properties of this triangle are collected on a separate page.
Solution 2
Let $A=(0,2),\,$ $B=(2,2),\,$ $C=(2,0),\,$ $D=(0,0).\,$ We find $P=(1,2-\sqrt{3})\,$ and $I=(1,2).\,$ Let $H\,$ be the orthocenter of $\Delta ADP.\,$ $H\,$ is the intersection of the lines $y=2-\sqrt{3}\,$ and $(2+\sqrt{3})x+y=2,\,$ so that $H=(2\sqrt{3}-3,2-\sqrt{3}).\,$ Let $O\,$ be the circumcenter of $\Delta ADP.\,$ Then $O=(x,1)\,$ and, since $OA=OP,\,$ $O=(2-\sqrt{3},1).$
But $L\,$ is the midpoint of $OH,\,$ implying $\displaystyle L=\left(\frac{\sqrt{3}-1}{2},\frac{3-\sqrt{3}}{2}\right).\,$ $IM\,$ has the slope of $1\,$ and $AM\,$ the slope of $-\sqrt{3}.\,$ Hence, $IM\,$ has the equation $y=x=1,\,$ while $AM\,$ has the equation $y=2-x\sqrt{3},\,$ from which $\displaystyle M=\left(\frac{\sqrt{3}-1}{2},\frac{1+\sqrt{3}}{2}\right).\,$
On the other hand, $K\,$ and $N\,$ are symmetric to $l\,$ and $M\,$ in line $x=1.\,$ Thus, $\displaystyle K=\left(\frac{5-\sqrt{3}}{2},\frac{3-\sqrt{3}}{2}\right).\,$ and $\displaystyle N=\left(\frac{5-\sqrt{3}}{2},\frac{1+\sqrt{3}}{2}\right).\,$
This completes the proof.
Solution 3
Solution 4
Let us choose an orthogonal coordinate system with origin at the point $I,\,$ the positive $X\,$ axis pointing to the right of the figure and the positive $Y\,$ axis pointing to the top. (If we show that points N and K have the same X coordinate, we are done.) From mirror symmetry of all the constructions about the axis $IP,\,$ $M\,$ and $L\,$ will be mirror images of $N\,$ and $K\,$ about the axis. Let the side of the square $ABCD\,$ be $2p.\,$ Thus, the coordinates of some of the points can be written as follows:
$I=(0,0),\,$ $B=(p,0),\,$ $C=(p,-2p),\,$ $P=(0,-p\tan 60^o).$
The coordinates for $P\,$ are deduced from the mirror symmetry and the fact that the $l(IP)/l(IB) = \tan 60^o$ $( \angle ABP = 60^o).\,$ From the mirror symmetry and $\angle MIN=90^o,\,$ we can deduce that $\angle BIN=45^o$.
Let the $l(IN)=q\,$ ($q\,$ is arbitrary). Thus, the coordinates of point $N\,$ can be written as
$N=(q\cos 45^o,-q\sin 45^o).$
The $X\,$ and $Y\,$ intercepts of line $BP\,$ are $p\,$ and $-p\tan 60^o,\,$ respectively. Thus, the equation of line $BP\,$ is
$\displaystyle \frac{x}{p}-\frac{y}{p\tan 60^o}=1.$
The coordinates of point $N\,$ need to satisfy this equation as the point $N\,$ lies on this line.Thus,
$\displaystyle \frac{q}{p}+\frac{q}{p\sqrt{3}}=\sqrt{2}.$
Thus, the $X\,$ coordinate of point $N\,$ $(=q\cos 45^o)\,$ is
$N_x = \displaystyle \frac{p}{1+1/\sqrt{3}}.$
The nine-point circle passes through the mid-points of the three sides which for $\triangle BPC\,$ are given by
$U=(p,-p),\,$ $V=\displaystyle \left(\frac{p}{2},-\frac{p\sqrt{3}}{2}\right),\,$ $W=\displaystyle \left(\frac{p}{2},-\frac{p}{2}(2+\sqrt{3})\right).$
Let the nine-point center $K\,$ have coordinates $(x,y).\,$ This point is equi-distant from points $U,\,$ $V,\,$ and $W.\,$ Hence,
$\displaystyle \begin{eqnarray} \left(x-p\right)^2+\left(y+p\right)^2&=&\left(x-\frac{p}{2}\right)^2+\left(y+\frac{p\sqrt{3}}{2}\right)^2 \\ \nonumber \left(x-p\right)^2+\left(y+p\right)^2&=&\left(x-\frac{p}{2}\right)^2+\left(y+\frac{p}{2}(2+\sqrt{3})\right)^2. \end{eqnarray}$
The quadratic terms in $x\,$ and $y\,$ cancel to give linear equations in $x\,$ and $y\,$ which when solved for $x\,$ gives
$\displaystyle x=p\frac{3-\sqrt{3}}{2}=\frac{p}{1+1/\sqrt{3}}=N_x.$
QED.
Acknowledgment
I am grateful to Leo Giugiuc for posting this Tran Quang Hung's problem at the CutTheKnotMath fcebook page. Proof of Lemma is by Amit Itagi; Solution 2 is by Leo Giugiuc; Solution 3 is by Takis Chronopoulos; Solution 4 is by Amit Itagi.
- Nine Point Circle: an Elementary Proof
- Feuerbach's Theorem
- Feuerbach's Theorem: a Proof
- Four 9-Point Circles in a Quadrilateral
- Four Triangles, One Circle
- Hart Circle
- Incidence in Feuerbach's Theorem
- Six Point Circle
- Nine Point Circle
- 6 to 9 Point Circle
- Six Concyclic Points II
- Bevan's Point and Theorem
- Another Property of the 9-Point Circle
- Concurrence of Ten Nine-Point Circles
- Garcia-Feuerbach Collinearity
- Nine Point Center in Square
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73608578
