García-Feuerbach Collinearity

What Might This Be About?

Statement

In $\Delta ABC,$ let $M_a,$ $M_b,$ $M_c,$ be the midpoints, $T_a,$ $T_b,$ $T_c$ the poits of tangency of the incircle $(I)$ on sides $BC,$ $AC,$ $AB,$ respectively. $F$ the Feuerbach point of $\Delta ABC;$ $M$ the midpoint of arc $M_aM_c$ of the 9-point circle; $D$ the midpoint of $BI.$

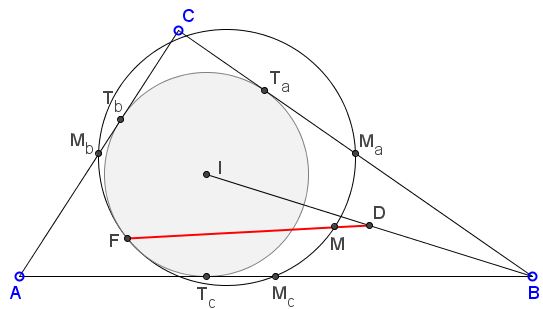
Garcia's collinearity - problem

The three points $F,$ $M,$ $D$ are collinear.

To remind, the Feuerbach point is the point of tangency of the incircle and the 9-point circle. The 9-point circle is, in particular, through the midpoints of the sides of a triangle.

The proof is mostly done by angle chasing and depends on three lemmas.

Lemma 1

Let $B'$ be the foot of the bisector of $\angle ABC.$

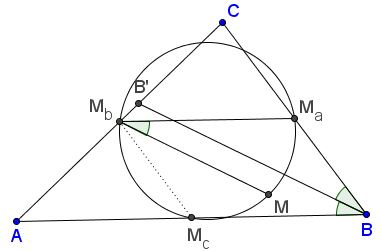
Garcia's collinearity - Lemma 1

Then $\angle M_{a}M_{b}M=\angle ABB'=\angle CBB'.$

Indeed, since $M_{a}M_{b}\parallel AB,$ $\angle M_{a}M_{b}M_{c}=\angle ABC.$ $\angle M_{a}M_{b}M=\frac{1}{2}\angle M_{a}M_{b}M_{c}$ as an angle inscribed into the 9-point circle and subtended by half of the arc $M_{a}M_{c}$ subtending $\angle M_{a}M_{b}M_{c}.$

Lemma 2

Let circle $(I)$ be inscribed into angle $ABC,$ and touching $BC$ at $T_a;$ $D$ the midpoint of $BI.$

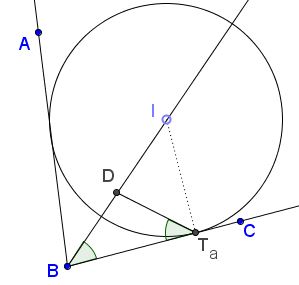
Garcia's collinearity - Lemma 2

Then $\angle T_{a}BD=\angle DT_{a}B.$

Indeed, $\angle BT_{a}I=90^{\circ},$ so $D$ is the circumcenter of the right triangle $BIT_a,$ making $\Delta BDT_a$ isosceles, with $\angle T_{a}BD=\angle DT_{a}B.$

Lemma 3

The 9-point circle of $\Delta BCI$ passes through the Feuerbach point of $\Delta ABC.$

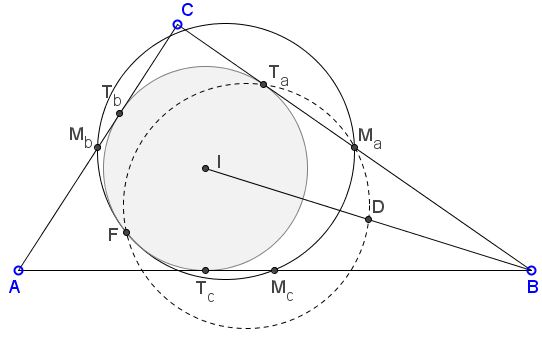
Garcia's collinearity - Lemma 3

This is Theorem 1 from [Jan Vonk, The Feuerbach point and reflections of the Euler line, Forum Geometricorum, 9 (2009) 47-55].

Proof

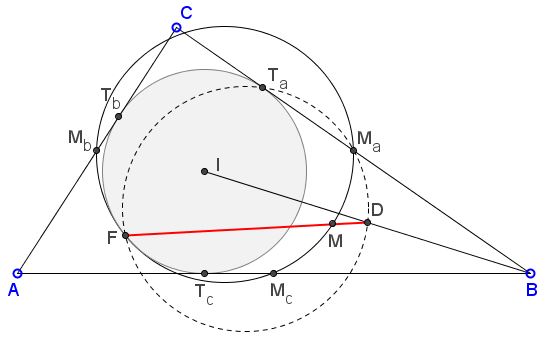
Garcia's collinearity - solution

$\angle M_{a}T_{a}D=\angle M_{a}FD=\angle CBI,\\ \angle M_{a}M_{b}M=\angle M_{a}FM=\angle CBI. $

It follows that $\angle M_{a}FM=\angle M_{a}FD,$ which exactly means that points $F,M,D$ are collinear.

Acknowledgment

The statement and its proof are due to Emmanuel Antonio José García (Dominican Republic).

72192139