Another Property of the 9-Point Circle
What Might This Be About?
Problem
In $\Delta ABC,$ $M_a$ is the midpoint of $BC;$ $H$ the orthocenter; $O$ the circumcenter; $N$ the center of the 9-point circle; $H_a,$ $H_b,$ $H_c$ are the feet of altitudes from $A,$ $B,$ $C,$ respectively; $S_a$ the midpoint of $AH;$ $R$ be the circumradius of $\Delta ABC.$
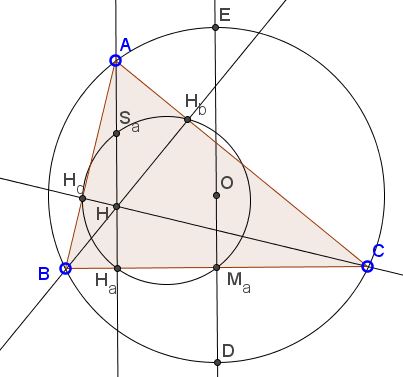
Let $ED\perp BC$ at $M_a,$ with $D$ and $E$ on the circumcircle $(ABC),$ as shown. Prove that $\displaystyle DM_{a}=R+\frac{AH}{2}$ and $\displaystyle EM_{a}=R-\frac{AH}{2},$ making
$AH^{2}=4R^{2}-a^2.$
Solution
The problem reduces to showing that $HM_{a}OS_{a}$ is a parallelogram, for then $OM_{A}=HS_{a}=AH/2.$ $(S_{a}$ is one of the nine points - an Euler point - that gave the 9-point circle its name.)
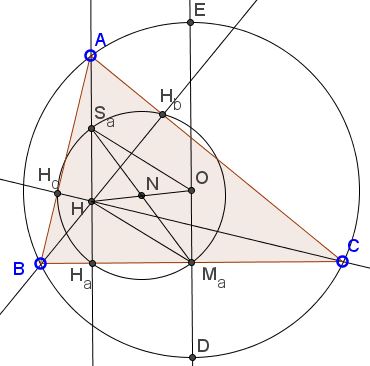
$N$ is the midpoint of $HO,$ whereas $M_{a}S_{a}$ is the diameter of $(N),$ - the 9-point circle - because $\angle M_{a}H_{a}S_{a}=90^{\circ}$ and all three points lie on $(N).$ The claim follows.
As a consequence (using the Intersecting Chords Theorem), $BM_{a}\cdot CM_{a}=DM_{a}\cdot EM_{a},$ so that
$\displaystyle\bigg(\frac{BC}{2}\bigg)^{2}=R^{2}-\frac{AH^2}{4},$
or,
$AH^{2}=4R^{2}-a^2.$
Acknowledgment
The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page.
- Nine Point Circle: an Elementary Proof
- Feuerbach's Theorem
- Feuerbach's Theorem: a Proof
- Four 9-Point Circles in a Quadrilateral
- Four Triangles, One Circle
- Hart Circle
- Incidence in Feuerbach's Theorem
- Six Point Circle
- Nine Point Circle
- 6 to 9 Point Circle
- Six Concyclic Points II
- Bevan's Point and Theorem
- Another Property of the 9-Point Circle
- Concurrence of Ten Nine-Point Circles
- Garcia-Feuerbach Collinearity
- Nine Point Center in Square
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573942
