The Shortest Crease
What this might be about?
18 October 2015, Created with GeoGebra
Problem
An interesting optimization problem has been offered by Henry Ernest Dudeney:
Fold a page, so that the bottom outside corner touches the inside edge and the crease is the shortest possible. That is about as simple a question as we could put, but it will puzzle a good many readers to discover just where to make the fold. I give two examples of folding:
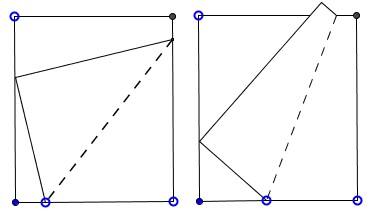
It will be seen that the crease on the right is longer than that on the left, but the latter is not the shortest possible.
References
Answer
Bisect $AB$ in $M.$ Bisect $AM$ at $E.$ Draw the line at $M$ perpendicular to $AB$ and the semicircle with diameter $BE.$ Let $N$ be the intersection of the two.
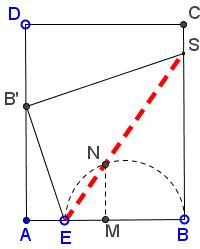
The line $EN$ gives the direction of the shortest possible crease under the conditions.
Solution
The solution below is straightforward application of the Pythagorean theorem and the very beginning of the calculus.
Taking into account that Dudeney "folds a page," assume $AD\gt AB=4.$ Denote $x=BE.$
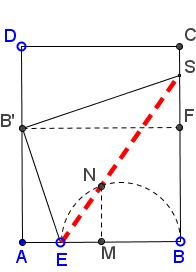
Then successively: $AE=4-x;$ $EB'=BE=x;$ $AB'=\sqrt{x^{2}-(4-x)^{2}}.$
Further, triangles $AEB'$ and $FSB'$ are similar so that $\displaystyle FS=\frac{AE\cdot B'F}{AB'}=\frac{4(4-x)}{\sqrt{x^{2}-(4-x)^{2}}};$
$\begin{align} BS&=BF+FS\\ &=\sqrt{x^{2}-(4-x)^{2}}+\frac{4(4-x)}{\sqrt{x^{2}-(4-x)^{2}}}\\ &=\frac{x^{2}-(4-x)^{2}+4(4-x)}{\sqrt{x^{2}-(4-x)^{2}}}\\ &=\frac{4x}{\sqrt{x^{2}-(4-x)^{2}}}\\ &=\frac{2x}{\sqrt{2(x-2)}}. \end{align}$
Finally
$\begin{align} ES^{2}&=BE^2+BS^2\\ &=x^{2}+\frac{4x^{2}}{2(x-2)}\\ &=\frac{x^{3}}{x-2}\\ \end{align}$
Consider the function $\displaystyle f(x)=\frac{x^{3}}{\sqrt{x-2}}.$
$\displaystyle f'(x)=\frac{3x^{2}(x-2)-x^{3}}{(x-2)^{2}}=\frac{2x^{2}(x-3)}{(x-2)^2}.$
$x=0$ leads to no crease, but $x=3$ does. We next find that $f''(3)\gt 0$ so that $x=3$ is a local minimum.
This shows why Dudeney's answer is correct. With $x=3,$ $MN=\sqrt{2}$ and $BS=3\sqrt{2},$ implying that $ES$ passes through $N.$ Thus Dudeney's answer is a byproduct of the calculus solution. It would be exciting to arrive at his result without calculus.
Thus, according to Dudeney the minimum crease of a page with base $4$ equals $3\sqrt{3}.$ This crease can be obtained for any page whose vertical size is at least $3\sqrt{2}.$ However, it is obvious that, with the vertical side $b\lt 3\sqrt{3},$ the vertical crease through the midpoint $M$ will be shorter than $3\sqrt{3}.$ Obviously, Dudeney assumed that, for a "page," the ratio of the vertical to the horizontal side exceeds $3\sqrt{3}/4.$
- An Interesting Example of Angle Trisection by Paperfolding
- Angle Trisection by Paper Folding
- Angles in Triangle Add to 180o
- Broken Chord Theorem by Paper Folding
- Dividing a Segment into Equal Parts by Paper Folding
- Egyptian Triangle By Paper Folding
- Egyptian Triangle By Paper Folding II
- Egyptian Triangle By Paper Folding III
- My Logo
- Paper Folding And Cutting Sangaku
- Parabola by Paper Folding
- Radius of a Circle by Paper Folding
- Regular Pentagon Inscribed in Circle by Paper Folding
- Trigonometry by Paper Folding
- Folding Square in a Line through the Center
- Tangent of 22.5o - Proof Without Words
- Regular Octagon by Paper Folding
- The Shortest Crease
- Fold Square into Equilateral Triangle
- Circle Center by Paperfolding
- Folding and Cutting a Square
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73608846
