Building a Bridge
What is this about?
A Mathematical Droodle
| Buy this applet What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Eye opener| |Store|
Copyright © 1996-2015 Alexander Bogomolny
This one is a basic optimization problem. It's well known and serves as an easy illustration of the usefulness of the simplest of geometric transforms - translation.
Two points A and B are given on opposite sides of a strip defined by two parallel lines. The strip represents a river, and the points two cities on the opposite sides of the latter. The problem is to build the shortest possible road between A and B, assuming that the land parts of the road are straight line segments and the bridge is perpendicular to the banks.
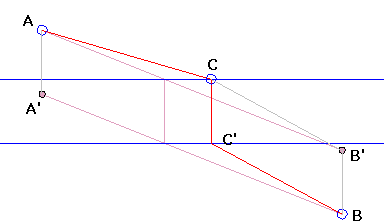
Let C be a point on the upper bank and C' its mate on the lower bank, so that CC' is perpendicular to both lines. CC' defines a vector V and a translation transform in the plane. It is clear that the length of V enters all possible choices of C on the upper bank. The problem is thus equivalent to minimizing the "land" sum
Translate point B by -V to obtain B'. By the triangle inequality,
AC + CB' ≥ AB',
while CB' = C'B. Therefore, the shortest route is defined by the position of C where the line AB' crosses the upper bank.
Clearly, we could have translated A by V to A' and considered intersection C' of A'B with the lower bank. The result would have been the same.
Note: the problem admits extensions to more than one river seperating the two cities. The case of two rivers is discussed elsewhere at the site.
References
- I. M. Yaglom, Geometric Transformations I, MAA, 1962
Related material
| |
A Sample of Optimization Problems II | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Eye opener| |Store|
Copyright © 1996-2015 Alexander Bogomolny| 49552211 |
