Area Optimization in Trapezoid
Introduction
On an earlier page, we had proved a result by Miguel Ochoa Sanchez concerning areas in a trapezoid:
In trapezoid $ABCD,\;$ with $AB\parallel CD,\;$ $P\in AB\;$ and $R\in CD;\;$ $Q=CP\cap BR,\;$ $S=AR\cap DP.$
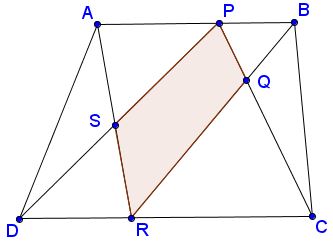
Prove that $[PQRS]\le\frac{1}{4}[ABCD],\;$ where $[X]\;$ denotes the area of shape $X.$
Marcello Tarquini has developed a refinement and a proof (Proof 1) discussed below. Proof 2 (from an affine perspective) is by Grégoire Nicollier.
Problem
Proof 1 relies on two simple lemmas.
Lemma 1
In trapezoid $ABCD,\;$ $V\in AD\;$ and $W\in BC,$ $VW\parallel AB\parallel CD;\;$ $O=AC\cap BD\in VW,$
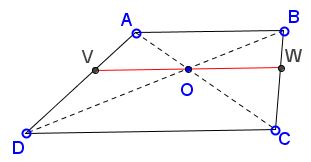
Then
$\displaystyle VW=2\cdot OW=\frac{2}{\displaystyle\frac{1}{AB}+\frac{1}{CD}}.$
This is to say that $VW\;$ is the harmonic mean of $AB\;$ and $CD.$
Lemma 2
Let $a,b,c,d\;$ be four positive real numbers. Then
$\displaystyle\frac{1}{\displaystyle\frac{1}{a}+\frac{1}{b}}+\frac{1}{\displaystyle\frac{1}{c}+\frac{1}{d}}\le\frac{1}{\displaystyle\frac{1}{(a+c)}+\frac{1}{(b+d)}},$
with the equality attained only for $\displaystyle\frac{a}{c}=\frac{b}{d}.$
For a proof see, wolframalpha.com.
Proof 1
Call $S',Q'\;$ the intersections with $PR\;$ of the parallels to $AB\;$ through $S\;$ and $Q,\;$ respectively.
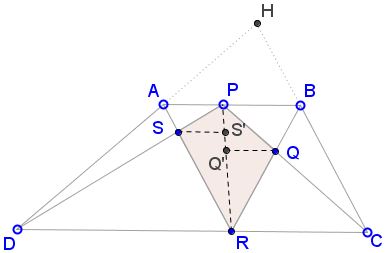
The area $[PQRS]\;$ is easily seen to be $[PQRS]=\frac{1}{2}h\cdot(SS'+QQ'),\;$ where $h\;$ is the height of the trapezoid. Since $h\;$ is constant, to maximize $[PQRS]\;$ suffice it to maximize $SS'+QQ'.$
By Lemma 1 (in the trapezoids $APRD\;$ and $BCRP,$
$\displaystyle SS'+QQ'=\frac{1}{\displaystyle\frac{1}{AP}+\frac{1}{DR}}+\frac{1}{\displaystyle\frac{1}{BP}+\frac{1}{CR}}.$
By Lemma 2,
$\displaystyle\begin{align}SS'+QQ' &=\frac{1}{\displaystyle\frac{1}{AP}+\frac{1}{DR}}+\frac{1}{\displaystyle\frac{1}{BP}+\frac{1}{CR}}\\ &\le\frac{1}{\displaystyle\frac{1}{AP+BP}+\frac{1}{CR+DR}}\\ &=\frac{1}{\displaystyle\frac{1}{AB}+\frac{1}{CD}}, \end{align}$
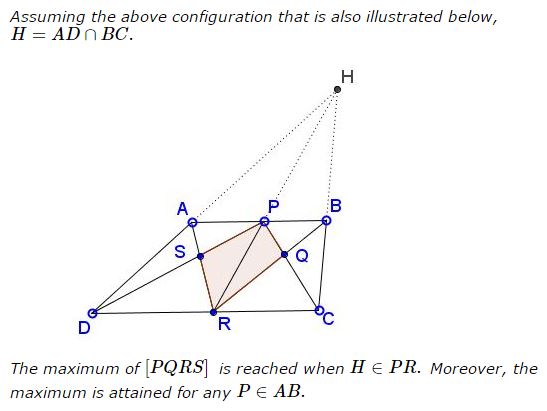
such that $\max (SS'+QQ')=\displaystyle\frac{1}{\displaystyle\frac{1}{AB}+\frac{1}{CD}},\;$ and is attained when $\displaystyle\frac{AP}{DR}=\frac{BP}{CR}\;$ which, by similarity, is equivalent to asking for $PR\;$ to pass through $H.$
Observe that by the AM-HM inequality,
$\displaystyle [SPQR]=\frac{h}{2}\frac{1}{\displaystyle\frac{1}{AB}+\frac{1}{CD}}\le \frac{h}{4}\cdot\frac{AB+CD}{2}=\frac{1}{4} [ABCD].$
Note 1: by Desargues' theorem in triangles $ARB,CPD,\;$ if $H\in PR,\;$ then $SQ\parallel AB\;$ such that, in this case, $S'=Q'$ and $SQ\parallel AB.\;$ The value of the maximum does not depend on $P\;$ and, therefore, $[PQRS]\;$ does not depend on $P,\;$ neither does $SQ.$
Note 2: The proof still works when $ABCD\;$ is a parallelogram, i.e., when $AB=CD,\;$ in which case the formula
$\displaystyle \max [PQRS]=\frac{h}{2}\frac{1}{\displaystyle\frac{1}{AB}+\frac{1}{CD}}$
becomes $\max [PQRS]=\frac{1}{4}[ABCD]\;$ when $PR\parallel AD\parallel BC.$
Proof 2
As affine transformations preserve collinearity, parallelism, and area ratios and as any two triangles are affinely equivalent, it suffices to consider the isosceles right-angled triangle $DCH\;$ with $D=(0,\,0),\;$ $C=(1,\,0)\;,$ and $H=(0,\,1).\;$ Setting $A=(0,\,a),\;$ $P=(p,\,a),\;$ $R=(r,\,0)$ with $0\lt a\lt 1,\;$ $0\le r\le1,\;$ and $0\le p\le1-a,\;$ one has then $B=(1-a,\,a),\;$
$\displaystyle S=\left(\frac{pr}{p+r},\,\frac{ar}{p+r}\right),$$ $$Q=\left(\frac{1-a-pr}{2-a-p-r},\,\frac{a(1-r)}{2-a-p-r}\right),$
and $[ABCD]=a-\frac{a^2}2.\;$ Using the vertice coordinates and $2\times2$-determinants, one finds
$\displaystyle [PQRS]=\frac{a\left((1-a)(p+r-r^2)-p^2\right)}{2(p+r)(2-a-p-r)}$
and thus
$\displaystyle \frac{[PQRS]}{[ABCD]}=\frac{1-a}{(2-a)^2}-\frac{(p-(1-a)r)^2}{(2-a)^2(2-a-p-r)(p+r)}$
is at most
$\displaystyle \frac{1-a}{(2-a)^2}$
and attains this value when the second term vanishes, that is, when $H\;$ is on the line $PR.\;$ As $\displaystyle \frac{1-a}{(2-a)^2}$ is strictly decreasing on $[0,\,1],\;$ $[PQRS]/[ABCD]$ is smaller than $1/4.\;$
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73579670
