An Unusual Problem by Leo Giugiuc
Problem
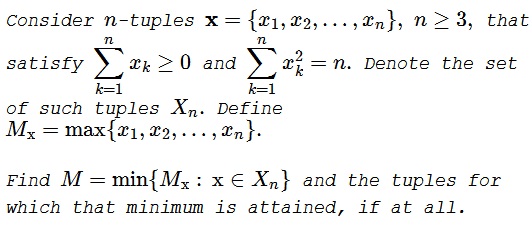
Lemma (Leo Giugiuc)
Let $s$ and $t$ be real numbers with $t\ge 0.$ Assume $\mathbf{x}\in X_n$ satisfies $\displaystyle \sum_{k=1}^{n}x_k=ns$ and $\displaystyle \sum_{k=1}^{n}x_k^2=n[s^2+(n-1)t^2].$ Then $M=s+t$ and this occurs at $\mathbf{x}=(s+t,s+t,\ldots,s+t,s-(n-1)t)$ and permutations.
The proof is left as a challenge to the reader.
Solution 1
From $n[s^2+(n-1)t^2]=n$ $\displaystyle t=\sqrt{\frac{1-s^2}{n-1}}.$ According to the lemma, the task is to minimize the function $\displaystyle f(s)=s+\sqrt{\frac{1-s^2}{n-1}}$ on $[0,1].$
We have $\displaystyle f'(s)=1-\frac{1}{\sqrt{n-1}}\cdot\frac{s}{\sqrt{1-s^2}}$ for $s\in [0,1).$ Clearly, the function $\displaystyle \frac{s}{\sqrt{1-s^2}}$ is strictly increasing on $[0,1),$ which makes $f'$ decreasing. Since $f'(0)=1\gt 0$ and $f'(1^{-})=-\infty\lt 0,$ we see that
$\displaystyle \min_{s\in [0,1]} f(s)\in\{f(0),f(1)\}=\frac{1}{\sqrt{n-1}}.$
By the lemma, that minimum is attained at $\displaystyle \mathbf{x}=\left(\frac{1}{\sqrt{n-1}},\frac{1}{\sqrt{n-1}},\ldots,\frac{1}{\sqrt{n-1}},-\sqrt{n-1}\right)$ and permutations.
Solution 2
Not quite a rigorous argument which requires a bit of imagination:
I answered a different question first, but the solution will be similar and easier to imagine.
Part 1
======
If we change $\max\{x_1,...,x_n\}$ to the max-norm $\max\{|x_1|,...,|x_n|\}=\|(x_1,...,x_n) \|_\infty$ then the question becomes:
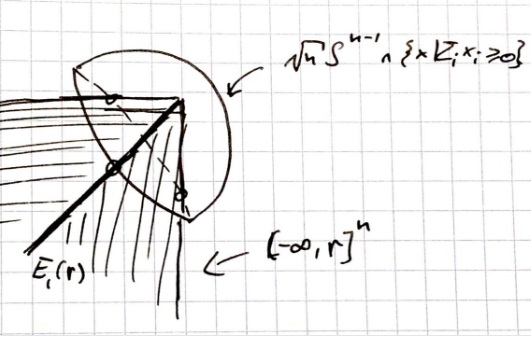
What is the smallest "radius" $r$ such that the hypercube $[-r,r]^n$ (which is the ball wrt. the max-norm) touches the hemisphere
$\displaystyle \sqrt{n}\mathbb{S}^{n-1} \cap \{ x \mid \sum_i x_i \geq 0 \}.$
Imagine that we start with $r=0$ and grow it.
Surely the vertices of the hypercube touch the sphere $\sqrt{n}\mathbb{S}^{n-1}$ first; then $r = 1$ and the vertices are $(\pm 1,...,\pm 1)$. Now we only need to make sure that there are more +1s than -1s to satisfy the condition $\sum_i x_i \geq 0$.
Part 2
======
The original problem is different in that we deal not with the hypercube but with the polyhedron $P_r := (-\infty,r]^n$. Again we start with $r=0$, in which case $P_0$ does not meet the hemisphere. When we grow $r$, then the edges of $P_r$, which are
$\displaystyle E_i(r) := \{ (r,...,r) - te_i \mid t \geq 0 \} \text{ for } i = 1,..,n $
meet the hemisphere first.
For example $E_1(r) = \{ (r-t,r,...,r) \mid t \geq 0 \}$. In fact, we can due to symmetry ask: What is the smallest $r$ such that the ray $E_1(r)$ meets the hemisphere? Surely if $E_1(r)$ meets the hemisphere, then it must meet it on its boundary $\mathbb{S}^{n-1}\cap \{x\mid \sum_i x_i = 0 \}.$ Therefore $(r-t)+r+...+r = 0$ which tells us $t = nr$.
Finally
$\displaystyle n=(t-r)^2+r^2+...+r^2 \iff n = (n-1)^2r^2 + (n-1)r^2 \iff r = \sqrt{\frac{n}{(n-1)^2+n-1}} = \sqrt{\frac{1}{n-1}}$
and the minimum is attained at
$\displaystyle (r-t,r,...,r) = \left((1-n)\sqrt{\frac{1}{n-1}},\sqrt{\frac{1}{n-1}},...,\sqrt{\frac{1}{n-1}}\right).$
Acknowledgment
The problem, with a solution (Solution 1), was kindly communicated to me by Leo Giugiuc. Leo wrote that the problem was inspired by problem 3 from The Ninth Nordic Mathematical Contest (1994). Solution 2 is by Long Huynh Huu.
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73564793
