Folding Square in a Line through the Center
The GeoGebra applet below is intended to illustrate a problem posed by @JamesTanton:
Fold a square piece of paper on a line that passes through center of the square. Which line produces least amount of overlapping area?
(The line can be moved by dragging the point that lies outside the square.)
|Mail| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Solution
Let's complement the figure with a few extra elements as shown:
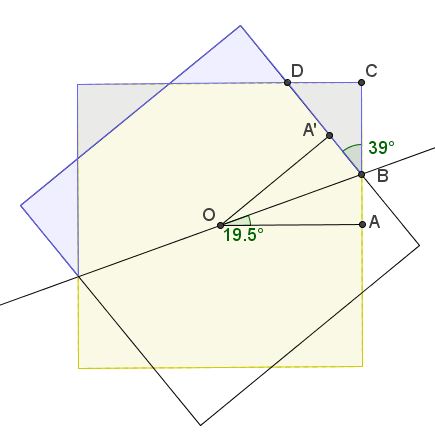
Assume the square has side length of 1. Denote \(\angle AOB = \alpha\), \(BC = y\), and \(CD = x\). An important observation is that \(\angle CBD = 2\alpha\). We have
\(\displaystyle\tan \alpha = \frac{1/2 - y}{1/2} = 1-2y\)
and
\(\displaystyle\tan 2\alpha = \frac{x}{y}.\)
Recollect the formula \(\displaystyle\tan 2\alpha = \frac{2\tan \alpha}{1-\tan ^{2}\alpha}\). Combining the three formulas gives
\(\displaystyle\frac{x}{y}=\frac{2(1-2y)}{1-(1-2y)^{2}}=\frac{1}{2}\frac{1-2y}{y-y^{2}}.\)
Thus we can express \(x\) in terms of \(y\):
\(\displaystyle x=\frac{1}{2}\frac{1-2y}{1-y}.\)
Now observe that due to the rotational and mirror symmetries of the diagram, all eight cutoff triangles are equal. The overlap whose area we have to find could be obtained from half the square (cutoff by the given line) by removing two of the triangles. The triangles in question are right with legs of length \(x\) and \(y\). The area of two of them is
\(\displaystyle f(y) = xy=\frac{1}{2}\frac{y(1-2y)}{1-y}.\)
The overlap has the least area when \(f(y)\) attains its maximum. Here's the graph of function \(f\):
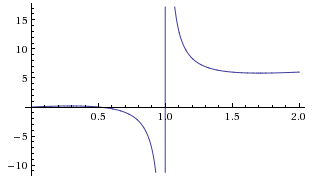
We are only concerned with its behavior on interval \((0,1)\), for \(1\le y\lt 1\). On that interval, the function has a single local maximum. To find it we differentiate:
\(\displaystyle f'(y) = \frac{1}{2}\frac{(1-4y)(1-y)-(-1)y(1-2y)}{(1-y)^{2}}.\)
The numerator simplifies two \(2y^{2}-4y+1\). The maximum is one of the roots of the quadratic equation
\(\displaystyle 2y^{2}-4y+1=0,\)
which are \(\displaystyle y_{1,2}=\frac{2\pm\sqrt{2}}{2}\). Of these, \(\displaystyle \frac{2-\sqrt{2}}{2}\) lies in the interval \((0,1)\). For this \(y\), if I am not seriously mistaken, \(\displaystyle x=\frac{2-\sqrt{2}}{2}\) so that \(x=y\) and the triangles are right isosceles. What this means is that the angle between the sides of the two squares is \(45^{\circ}\), while the line form angle of \(22.5^{\circ}\) with the horizontal side. This is natural enough and may have a proof that does not use derivatives. I would like to see such one.
Here it is!
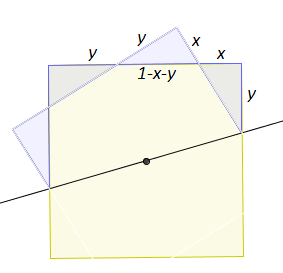
Using the same notations as before, the top horizontal side of the stationary square equals \(x + y + \sqrt{x^{2}+y^{2}}=1\), from which \(2(x+y)=1+2xy\). It follows that \(xy\) and \(x+y\) attain their maxima simultaneously at the point where \(1-x-y\) attains minimum. But the latter is the hypotenuse of the right triangle with legs \(x\) and \(y\). If the area of that triangle is the greatest possible while the base is the least possible, then the altitude to the hypotenuse ought to be at maximum to compensate for the shortness of the hypotenuse. The altitude is clearly at maximum when the sides of the squares are at \(45^{\circ}\).
Observe in passing that we may express \(x\) in terms of \(y\) from \(2(x+y)=1+2xy\). The result is satisfyingly \(\displaystyle x=\frac{1}{2}\frac{1-2y}{1-y}\) as before.
So for the minimal overlap \(\displaystyle x=y=\frac{2-\sqrt{2}}{2}\), while the area of the overlap is \(\displaystyle A=\frac{1}{2}-2\frac{xy}{2}\) which gives the minimum value
\( \displaystyle \begin{array}{4,2} A&=\frac{1}{2}-(\frac{2-\sqrt{2}}{2})^{2} \\ &=\frac{1}{2}-\frac{6-4\sqrt{2}}{4} \\ &=\frac{1-3+2\sqrt{2}}{2} \\ &=\sqrt{2}-1. \end{array} \)
This area can be computed differently. The intersection of two squares at \(45^{\circ}\) to each other is a regular octagon with area \(\displaystyle 8\frac{1}{2}\frac{1}{2}(\sqrt{2}-1)=2(\sqrt{2}-1)\).
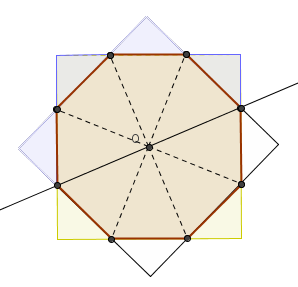
The area of the overlap is exactly one half of the area of the octagon, i.e., \(\displaystyle \sqrt{2}-1\).
- An Interesting Example of Angle Trisection by Paperfolding
- Angle Trisection by Paper Folding
- Angles in Triangle Add to 180o
- Broken Chord Theorem by Paper Folding
- Dividing a Segment into Equal Parts by Paper Folding
- Egyptian Triangle By Paper Folding
- Egyptian Triangle By Paper Folding II
- Egyptian Triangle By Paper Folding III
- My Logo
- Paper Folding And Cutting Sangaku
- Parabola by Paper Folding
- Radius of a Circle by Paper Folding
- Regular Pentagon Inscribed in Circle by Paper Folding
- Trigonometry by Paper Folding
- Folding Square in a Line through the Center
- Tangent of 22.5o - Proof Without Words
- Regular Octagon by Paper Folding
- The Shortest Crease
- Fold Square into Equilateral Triangle
- Circle Center by Paperfolding
- Folding and Cutting a Square
|Mail| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
