Trigonometry by Paper Folding

Given a square piece of paper, prove using just three folds the trigonometric identity:

$\arctan 1 + \arctan 2 + \arctan 3 = \pi.$

We need to prove the following:

$\arctan 1 + \arctan 2 + \arctan 3 = \pi.$

With the notation as in the diagram below, make three folds: $BD,$ $EF,$ $(E$ and $F$ are the midpoints of $AB$ and $CD,$ respectively), and $EC.$

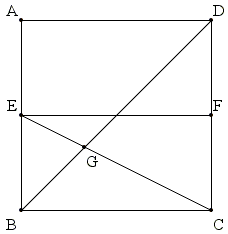
arctan 1 + arctan 2 + arctan 3 = pi, #1

From $\Delta BCE,$ $\angle BEG = \angle ECF = \arctan 2.$ From $\Delta ABD,$ $\angle EBG = \angle ABD = \arctan 1.$ To establish the assertion, we only need to show that $\angle BGE = \arctan 3,$ for then in $\Delta BEG$ the angles are exactly $\arctan 1,$ $\arctan 2,$ $\arctan 3.$

Imagine adding a diagonal $AC$ and mark the center of the square $H.$ $H$ lies on $AC,$ $BD,$ and $EF.$

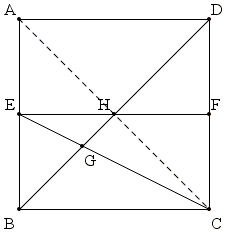
arctan 1 + arctan 2 + arctan 3 = pi, #1

In $\Delta ABC,$ $BH$ and $CE$ are two medians and $G$ is the centroid. $G$ divides the medians in the ratio $2:1.$ It follows that $GH = BH/3.$ In $\Delta CGH,$ $CH = BH = 3\times GH,$ implying $\angle BGE = \angle CGH = \arctan 3.$

Note: Grégoire Nicollier has observed that the true reason for $\arctan 1 + \arctan 2 + \arctan 3 = \pi$ is that $1+2+3=1\times 2\times 3,$ as a consequence of the following identity

$\displaystyle\tan(\alpha+\beta+\gamma)=\frac{\tan\alpha+\tan\beta+\tan\gamma-\tan\alpha\tan\beta\tan\gamma}{1-\tan\alpha\tan\beta-\tan\alpha\tan\gamma-\tan\beta\tan\gamma}.$

Note: Elsewhere we offer an outlook that makes the just proved identity remarkably obvious; yet somewhere else we prove another curiosity: $\arctan (1/2) + \arctan (1/3) = \arctan 1.$

References

Michael W. Ecker, arctan 1 + arctan 2 + arctan 3 = π, College Mathematics Journal, VOL. 37, NO. 3, MAY 2006, pp. 218-219

Paper Folding Geometry

71872999