Problem 4033 from Crux Mathematicorum
Problem
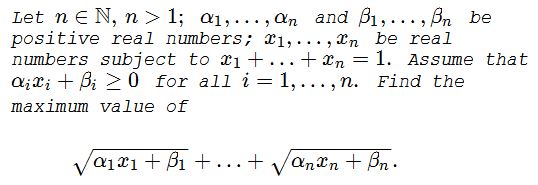
Solution 1
By the Cauchy-Schwarz inequality,
$\displaystyle\begin{align} \sum_{i=1}^n\sqrt{\alpha_ix_i+\beta_i}&=\sum_{i=1}^n\left(\sqrt{\alpha_i}\cdot\sqrt{x_i+\frac{\beta_i}{\alpha_i}}\right)\\ &\le\sqrt{\sum_{i=1}^n\alpha_i\cdot\sum_{i=1}^n\left(x_i+\frac{\beta_i}{\alpha_i}\right)}\\ &=\sqrt{\sum_{i=1}^n\alpha_i\cdot\left(1+\sum_{i=1}^n\frac{\beta_i}{\alpha_i}\right)}. \end{align}$
Equality holds if and only if
$\displaystyle \frac{\displaystyle x_1+\frac{\beta_1}{\alpha_1}}{\alpha_1}=\cdots=\frac{\displaystyle x_n+\frac{\beta_n}{\alpha_n}}{\alpha_n}=t,$
for some non-negative real $t.\,$ It follows that $\displaystyle x_i=t\alpha_i-\frac{\beta_i}{\alpha_i},\,$ for all $i=1,\ldots,n.\,$ Adding up gives
$\displaystyle 1=\left(\alpha_1+\ldots+\alpha_n\right)t-\left(\frac{\beta_1}{\alpha_1}+\cdots+\frac{\beta_n}{\alpha_n}\right)$
from which $\displaystyle t=\frac{\displaystyle 1+\sum_{i=1}^n\frac{\beta_i}{\alpha_i}}{\displaystyle\sum_{i=1}^n\alpha_i}.$ To sum up, the sought maximum is $\displaystyle \sqrt{\sum_{i=1}^n\alpha_i\cdot\left(1+\sum_{i=1}^n\frac{\beta_i}{\alpha_i}\right)}$ which is attained for $\displaystyle x_{k}=\frac{\alpha_k}{\displaystyle\sum_{i=1}^n\alpha_i}\cdot\left(1+\sum_{i=1}^n\frac{\beta_i}{\alpha_i}\right)-\frac{\beta_k}{\alpha_k},\,$ $k=1,\ldots,n.$
Solution 2
Let $y_k = \sqrt{\alpha_k x_k+\beta_k}$ for $k = 1,2,\dotsc,n$. Then $x_k = y_k^2/\alpha_k-\beta_k/\alpha_k$. The problem can then be restated in terms of $y_k$ as
Find the maximum value of $\displaystyle\sum_{k=1}^n y_k$ such that
$\displaystyle\begin{align} &y_k \geq 0 \textrm{ for all }k = 1,\dotsc,n\\ & \sum_{k=1}^n \frac{y_k^2}{\alpha_k} = \sum_{k=1}^n \frac{\beta_k}{\alpha_k} +1\\ \end{align}$
From the Cauchy-Schwarz inequality, we conclude that
$\displaystyle\begin{align} \sum_{k=1}^n y_k & = \sum_{k=1}^n \frac{y_k}{\sqrt{\alpha_k}} \sqrt{\alpha_k} \\ & \leq \sqrt{\sum_{k=1}^n \left(\frac{y_k}{\sqrt{\alpha_k}}\right)^2} \sqrt{\sum_{m=1}^n (\sqrt{\alpha_m})^2} \\ & = \sqrt{\sum_{k=1}^n \frac{y_k^2}{\alpha_k} \sum_{m=1}^n \alpha_m} \\ & = \sqrt{\left(\sum_{k=1}^n \frac{\beta_k}{\alpha_k} +1\right) \sum_{m=1}^n \alpha_m} \\ \end{align}$
with the equality happening when $\displaystyle\frac{y_k}{\sqrt{\alpha_k}} = \lambda \sqrt{\alpha_k}$ for all $k = 1,\dotsc,n,$ i.e., $x_k = \lambda^2 \alpha_k-\beta_k/\alpha_k$. Since $y_k \geq 0$, $\lambda \geq 0$. In addition, from $\displaystyle\sum_{k=1}^n x_k = 1$, it follows that $\displaystyle\lambda = \left(\sqrt{\sum_{k=1}^n\frac{\beta_k}{\alpha_k}+1}\right)\frac{1}{\displaystyle\sqrt{\sum_{k=1}^n\alpha_k}}$
Acknowledgment
The problem which is by Salem Malikic was published as #4033 by the Crux Mathematicorum. The problem and the solution were kindly sent to me by Leo Giugiuc. Solution 2 is by Shyam Subramanian.
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73578847
