Egyptian Triangle By Paper Folding II

A rectangular sheet of paper is folded so that one corner bisects the shorter side. Triangles I and II are congruent. If the length of the shorter side is \(8,\) find the length of the longer side.

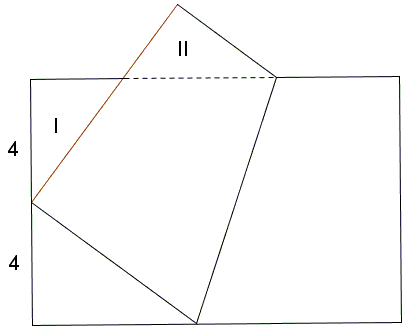
This is a problem from a 2011 olympiad for the seventh (the USA eighth) grade at the Moscow State University.

Solution

References

I. Yashchenko, Invitation to a Mathematical Festival, MSRI/AMS, 2013

Paper Folding Geometry

A rectangular sheet of paper is folded so that one corner bisects the shorter side. Triangles I and II are congruent. If the length of the shorter side is 8, find the length of the longer side.

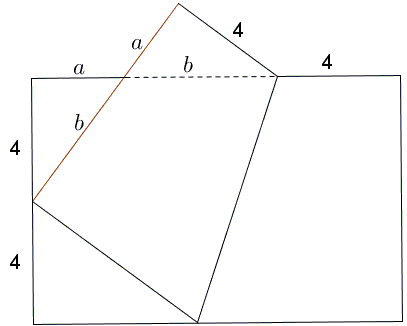
3:4:5 triangle by paper folding

It's convenient to introduce segment lengths \(a\) and \(b,\) as in the diagram. The folded short side of the rectangle is \(a+b=8\) so that the long side is \(a+b+4=12.\)

The right triangles I and II are of interest in their own right. Each has one leg equal to \(4\) and the sum of the other leg and hypotenuse \(8.\) You'd guess it straight away what triangle it is, but to make sure let's use the Pythagorean theorem:

\(4^{2}+a^{2}=(8-a)^2,\)

which leads to \(16=64-16a,\) or \(a=3\), implying the famous Egyptian 3-4-5 triangle. The dimensions of the rectangle - \(8\times 12\) - suggest an easy paper-folding construction of such a triangle which would start with first getting a not too wide a piece of paper, folding a square and then getting two more, which would lead to a rectangle of relative dimensions \(2\times 3.\)

a 2x3 rectangle by paper folding

71931231