A Problem with a Magical Solution from Secrets in Inequalities
Problem
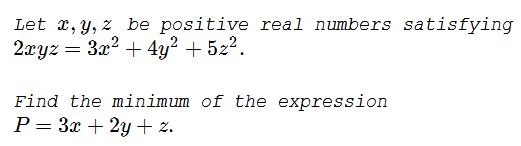
Solution
Let $a=3x,\,$ $b=2y,\,$ $c=z.\,$ Then $P=3x+2y+z=a+b+c\,$ and $a^2+3b^2+15c^2=abc.\,$
We'll make a double application of the weighted AM-GM inequality:
$\displaystyle \frac{\sum w_kx_k}{\sum w_k}\ge\sqrt[\sum w_k]{\prod x_k^{w_k}}.$
First, with $\displaystyle w_1=\frac{1}{2},\,$ $w_2=\frac{1}{3},\,$ $w_3=\frac{1}{6}\,$ $(w_1+w_2+w_3=1!),$
(1)
$\displaystyle a+b+c\ge (2a)^{\frac{1}{2}}(3b)^{\frac{1}{3}}(6c)^{\frac{1}{6}}.$
Then, with $\displaystyle w_1=\frac{1}{4},\,$ $\displaystyle w_2=\frac{3}{9}=\frac{1}{3},\,$ $\displaystyle w_3=\frac{15}{36}=\frac{5}{12}\,$ $(w_1+w_2+w_3=1!),$
(2)
$\displaystyle\begin{align}a^2+3b^2+15c^2&\ge (4a^2)^{\frac{1}{4}}(9b^2)^{\frac{3}{9}}(36c^2)^{\frac{15}{36}}\\ &=(4a^2)^{\frac{1}{4}}(9b^2)^{\frac{1}{3}}(36c^2)^{\frac{5}{12}}. \end{align}$
Multiplying (1) and (2),
$\displaystyle (a+b+c)(a^2+3b^2+15c^2)\ge 36abc,$
which implies $a+b+c\ge 36,\,$ the quantity that is attained for $x=y=z=6,\,$ making it the sought minimum.
Acknowledgment
This is problem #81 from Phan Kim Hungs' Secrets in Inequalities, (GIL Publishing House, 2007). I am grateful to Dan Sitaru who mailed me the problem and helped understand its solution.
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73574652
