An Inequality and Its Modifications
Problem
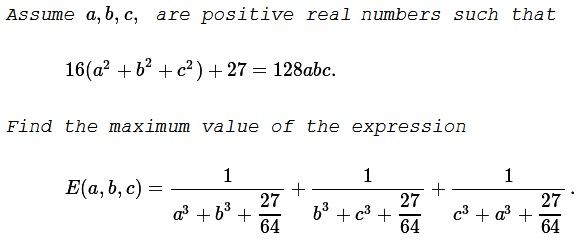
Solution
Note that from
$\displaystyle\begin{align}\sum_{cycl}(4a-3)^2 &= 16\sum_{cycl}a^2+27-24\sum_{cycl}a\\ &=128abc-24(a+b+c) \end{align}$
it follows that $128abc-24(a+b+c)\ge 0,\,$ or,
$\displaystyle\frac{128}{24}\ge\frac{a+b+c}{abc},$
i.e.,
$\displaystyle\frac{16}{3}\ge\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}.$
Now, by the AM-GM inequality, $\displaystyle a^3+b^3+\frac{27}{64}\ge 3\sqrt[3]{\frac{27a^3b^3}{64}}=\frac{9ab}{4}.\,$ Thus,
$\displaystyle\begin{align} E&=\sum_{cycl}\frac{1}{a^3+b^3+\displaystyle\frac{27}{64}}\\ &\le\sum_{cycl}\frac{4}{9ab}\\ &\le\frac{4}{9}\cdot\frac{16}{3}\\ &=\frac{64}{27}. \end{align}$
However, $\displaystyle E\left(\frac{3}{4},\frac{3}{4},\frac{3}{4}\right)=\frac{64}{27}\,$ such that $E\,$ attains its maximum at $a=b=c=\displaystyle\frac{3}{4}.$
Modification
Assume $a,b,c,\;$ are positive real numbers such that
$\displaystyle a^2+b^2+c^2+\frac{3}{4}=12abc.$
Prove that
$\displaystyle \frac{1}{a^3+b^3+\displaystyle\frac{1}{8}}+\frac{1}{b^3+c^3+\displaystyle\frac{1}{8}}+\frac{1}{c^3+a^3+\displaystyle\frac{1}{8}}\le 8.$
Generalization
Assume $a,b,c,\;$ are positive real numbers and $p\,$ a positive constant such that
$\displaystyle a^2+b^2+c^2+3p^2=\frac{6}{p}abc,$
Prove that
$\displaystyle \frac{1}{a^3+b^3+p^3}+\frac{1}{b^3+c^3+p^3}+\frac{1}{c^3+a^3+p^3}\le\frac{1}{p^3}.$
Equality is only achieved for $a=b=c=p.$
Acknowledgment
The problem above (from the Romanian Mathematical Magazine, #JP037, posed December 12, 2016) has been kindly posted at the CutTheKnotMath facebook page by Dan Sitaru, along with the solution by Kevin Soto Palacios (Peru). The problem has been proposed by Iuliana Trașcă and Neculai Stanciu (Romania).
Kunihiko Chikaya has posted (June 26, 2012) a similar problem (Modification) at the artofproblemsolving.com forum, followed by a slew of original solutions. On December 13, 2016, Kunihiko Chikaya has shared on the facebook a generalization (Generalization)
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73615506
