A 2-Variable Optimization From a China Competition
Problem
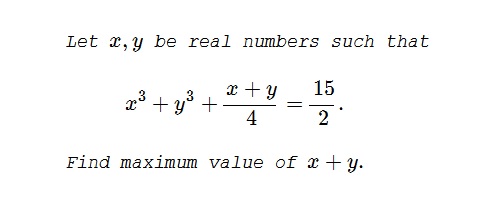
Solution 1
Let's first remark that the function $f(s)=4s^3+s$ is strictly increasing on the real line. Define $x+y=s$ and $xy=p.$ Clearly, $s^2\ge p,$ with equality only if $x=y=s$ and the constraint becomes
$16s^3-12sp+s=15.$
If $s\ge 0,$ then $-12s^3\le 12sp,$ implying $4s^3+s\le 15,$ or $\displaystyle s\le\frac{3}{2}.$
If $s\le 0,$ then $-12s^3\ge -12sp,$ implying $4s^3+3\le 15,$ which is impossible due to the above remark.
It follows that the maximum of $x+y$ is $3,$ attained for $\displaystyle x=y=\frac{3}{2}.$
Solution 2
$4p^3-12pq+p-30=0.$
Now, if $p\ge 0,$ then $p^3 \ge 4pq,$ i.e., $3p^3-12pq\ge 0,$ so that $p^3+p-30\le 0.$ But $p^3+p-30=(p-3)(p^2+3p+10).$ Since for all real $p,$ $p^2+3p+10\gt 0,$ $p^3+p-30\le 0,$ only if $p\le 3,$ with a maximum possible value of $p=3.$
If $p\lt 0,$ we have instead $(p-3)(p^2+3p+10)\gt 0,$ i.e., $p\gt 3$ in contradiction with $p\lt 0.$
Thus the maximum of $\max (x+y)=3.$ It is attained when there's equality in $p^2\ge 4q,$ i.e., when $x=y.$ Thus $\displaystyle x=y=\frac{3}{2}.$
Solution 3
Let $p=x+y$ and $q=x-y$.
$\displaystyle \begin{align} &x^3+y^3+\frac{x+y}{4}=\frac{15}{2} \\ &\left(\frac{p+q}{2}\right)^3+\left(\frac{p-q}{2}\right)^3+\frac{p}{4}=\frac{15}{2} \\ &p^3+p(3q^2+1)-30=0 \\\\ &q=\pm\sqrt{\frac{(3-p)\left[(p+3/2)^2+31/4\right]}{3p}}. \end{align}$
For $q$ to be real, $p\gt 0$ and $3-p\geq 0$, or $p\lt 0$ and $3-p\leq 0$. The second set has no real solution. The first set gives $3\geq p\gt 0$. Thus, the greatest value of $p$ is $3$. For this value of $p$, $q=0$ and $x=y=3/2$.
Solution 4
We shall employ Lagrange Multipliers.
Let $f(x,y) = x + y$ and $\displaystyle g(x,y) = x^3 + y^3 + {x + y \over 4} - {15 \over 2}$.
$\displaystyle \nabla f = \lambda \nabla g \Rightarrow \langle 1, 1 \rangle = \left\langle 3x^2 + {1 \over 4}, 3y^2 + {1 \over 4} \right\rangle \lambda$
We need to solve the following system of equations:
$\begin{align*} \left( 3x^2 + {1 \over 4} \right) \lambda = 1 \tag{1} \\ \left( 3y^2 + {1 \over 4} \right) \lambda = 1 \tag{2} \\ x^3 + y^3 + {1 \over 4}(x+y) = {15 \over 2} \tag{3} \end{align*}$
Subtract (1) from (2) to obtain:
$\begin{align*} \left( 3y^2 + {1 \over 4} \right) \lambda - \left( 3x^2 + {1 \over 4} \right) \lambda &= 1 - 1 \\ \left( 3y^2 - 3x^2 \right) \lambda &= 0 \qquad \Rightarrow 3y^2 = 3x^2 \Rightarrow \boxed{ x = y } \text{ and } \boxed{ x = -y } \end{align*}$
The $x = -y$ solution leads to a contradiction in the constraint equation ($0 = 15/2$), so we discard it. Applying $x = y$ to (3) gives:
$\displaystyle \begin{align*} x^3 + y^3 + {x + y \over 4} = {15 \over 2} \qquad \Rightarrow x^3 + x^3 + {x + x \over 4} &= {15 \over 2} \\ 4x^3 + x - 15 &= 0 \qquad \text{therefore } \boxed{ x = 1.5 } \end{align*}$
The maximum value of $x + y$ is $1.5 + 1.5 = 3$.
Extra
Let $x,y$ be real numbers such that
$\displaystyle x^3+y^3+\frac{x+y}{4}=\frac{15}{2}.$
Find the range of values of $x+y.$
As in Solution 1, set $x+y=2s$ and $xy=p.$ Above we proved that $\displaystyle 0\le s\le\frac{3}{2}.$ From $16s^3-12sp+s=15,$ $p=\displaystyle \frac{16s^3+s-15}{12s},$ which holds for $\displaystyle s\in\left(0,\frac{3}{2}\right].$ The expression defines function $f:\,\left(0,\frac{3}{2}\right]\to\left(-\infty,\frac{9}{4}\right].$ Function $f$ is increasing and bijective, moreover, as was shown in Solution 1, $\displaystyle \forall s\in\left(0,\frac{3}{2}\right],$ $f(s)\le s^2.$
It follows that the equation $\displaystyle t^2-2st+\frac{16s^3+s-15}{12s}=0$ admits two real solutions $x$ and $y$ that satisfy $\displaystyle x^3+y^3+\frac{1}{4}(x+y)=\frac{15}{2}.$ Thus, $0\lt (x+y)\le \frac{3}{2}.$ Naturally, there is no solution for s=0 as that would mean $0=15.$
Acknowledgment
The problem has been kindly posted to the CutTheKnotMath facebook page by Leo Giugiuc, along with the original link to The Art Of Mathematics facebook group. Solution 1 is by Leo Giugiuc; Solution 3 is by Amit Itagi; Solution 4 is by Gabriel Leitao.
Leo Giugiuc came up with the Extra problem of finding the lowest possible value of $x+y$ that satisfies the given constraint. The solution is by Leo Giugiuc.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73517919
