Fold Square into Equilateral Triangle
Problem
An interesting optimization problem has been offered by Henry Ernest Dudeney:
Take a perfectly square piece of paper, and so fold it as to form the largest possible equilateral triangle.
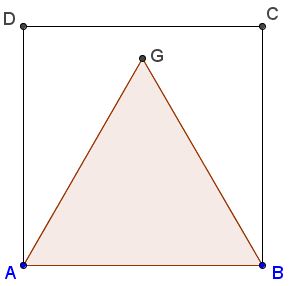
A triangle in which the sides are the same length as those of the square, as shown in the diagram, will not be the largest possible. Of course, no markings or measurements may be made except by the creases themselves.
References
Solution
We shall first establish the location of the largest equilateral triangle inscribed into a square and then demonstrate how this triangle can be obtained by folding the square. The argument for the former task is mainly intuitive.
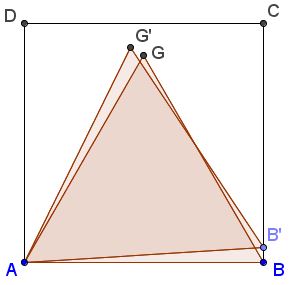
First of all, Dudeney is right claiming that the triangle with sides equal to those of the square can be the largest possible. Indeed, moving slightly one of the corners of the triangle along the side of the square, while keeping two of their corners fixed, will increase the side and hence the area of the triangle and keep its third vertex within the square:
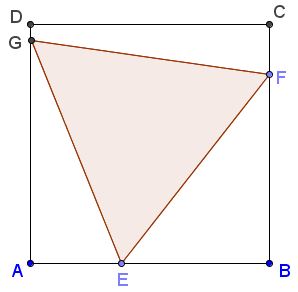
In a similar vein, we may claim that exactly on of triangle's vertices should coincide with one of the square's. Assume that this is not so:
Then the triangle can be slid to place one of its vertices into one of the square's corners:
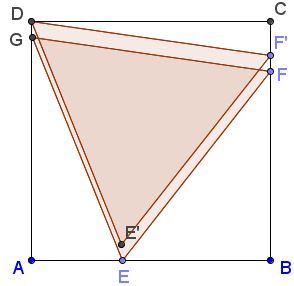
This would allow - as before - to slide one of the other vertices of the triangle, thus, increasing its side length and the area:
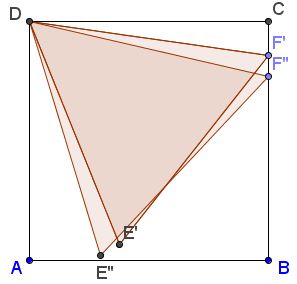
Construction
Dudeney offers the following procedure:
Fold the square in half and make the crease $IH.$ Fold the side $AB$ so that the point $B$ lies on $IH,$ and you will get the points $E$ and $F$ from which you can fold $FEG.$ While $B$ is on $E,$ fold $AB$ back on $AE,$ and you will have the line $AK.$ You can now fold the triangle $AGK,$ which is the largest possible equilateral triangle obtainable.
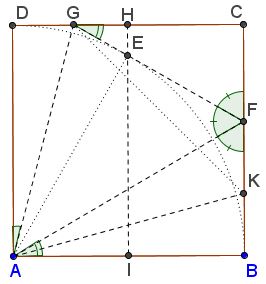
Preliminary
From the above it is clear that the largest equilateral triangle inscribed into a square is bound to have one vertex at a corner of the square and the other two on the two sides not adjacent to that vertex. Further, for the triangle $AGK$ to be equilateral we need $AG=AK,$ implying $\angle BAK=DAG=15^{\circ}$ because $\angle GAK=60^{\circ}.$
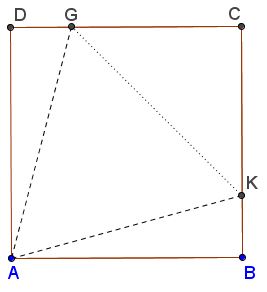
What is need is to show that, if $\angle BAK=DAG=15^{\circ},$ then $GK=AK.$
$\displaystyle\sin 15^{\circ}=\frac{\sqrt{6}-\sqrt{2}}{4},$ $\displaystyle\cos 15^{\circ}=\frac{\sqrt{6}+\sqrt{2}}{4},$ $\displaystyle\tan 15^{\circ}=2-\sqrt{3}.$
Assuming $AB=1,$ $\displaystyle AK=\frac{4}{\sqrt{6}+\sqrt{2}}=\sqrt{6}-\sqrt{2},$ $BK=2-\sqrt{3},$ $CK=CG=\sqrt{3}-1.$ It follows that $GK=\sqrt{2(\sqrt{3}-1)^{2}}=\sqrt{6}-\sqrt{2}=AK.$
Proof
It remains to be shown that Dudeney's folding really leads to the configuration where $AGK$ is equilateral.

When $B$ is folded onto $E\in IH,$ $AE=2AI,$ so that $\angle BAE=60^{\circ}$ and, therefore, $\angle BAF=30^{\circ}.$ Further, angles $BFA,$ $AFG,$ $CFG$ are all $60^{\circ}.$ $\displaystyle BF=\tan 30^{\circ}=\frac{\sqrt{3}}{3},\;$ $\displaystyle CF=1-\frac{\sqrt{3}}{3}=\frac{3-\sqrt{3}}{3}.\;$ $CG=CF\tan 60^{\circ}:$
$\displaystyle CG=\frac{3-\sqrt{3}}{3}\sqrt{3}=\sqrt{3}-1=CK,$
as required.
- An Interesting Example of Angle Trisection by Paperfolding
- Angle Trisection by Paper Folding
- Angles in Triangle Add to 180o
- Broken Chord Theorem by Paper Folding
- Dividing a Segment into Equal Parts by Paper Folding
- Egyptian Triangle By Paper Folding
- Egyptian Triangle By Paper Folding II
- Egyptian Triangle By Paper Folding III
- My Logo
- Paper Folding And Cutting Sangaku
- Parabola by Paper Folding
- Radius of a Circle by Paper Folding
- Regular Pentagon Inscribed in Circle by Paper Folding
- Trigonometry by Paper Folding
- Folding Square in a Line through the Center
- Tangent of 22.5o - Proof Without Words
- Regular Octagon by Paper Folding
- The Shortest Crease
- Fold Square into Equilateral Triangle
- Circle Center by Paperfolding
- Folding and Cutting a Square
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73600757
