Greatest Difference in Arithmetic Progression
Problem
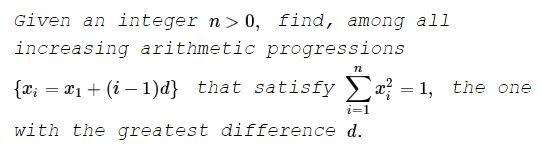
Solution 1
For $n=1\;$ or $n=2\;$ the problem is readily solvable. Assume $n\ge 3\;$ and consider two cases:
$n\;$ is odd
$n=2k+1,\;$ $k\ge 1.\;$ Let $x_k=x,\;$ $x_{k-i}=x-di,\;$ $x_{k+i}=x+di,\;$ $i=1,2,\ldots,k.\;$ Then
$\displaystyle\begin{align} 1 &= \sum_{i=1}^{n}x_i^2\\ &= x^2+\sum_{i=1}^{k}(x-di)^2+\sum_{i=1}^{k}(x+di)^2\\ &=(2k+1)x^2+2d^2\sum_{i=1}^{k}i^2\\ &=(2k+1)x^2+d^2\frac{(k+1)k(2k+1)}{3}\\ &= nx^2+d^2\frac{(n^2-1)n}{12} \end{align}$
from which $\displaystyle d=\sqrt{\frac{12}{(n^2-1)n}(1-nx^2).}\;$ The maximum $d$ is obtained for $x=0:$
$\displaystyle d=\sqrt{\frac{12}{(n^2-1)n}}.$
Then
$\displaystyle x_1=-\frac{n-1}{2}\sqrt{\frac{12}{(n^2-1)n}}=-\sqrt{\frac{3(n-1)}{n(n+1)}}.$
$n\;$ is even
$n=2k,\;k\ge 2.\;$ Let $\displaystyle x=\frac{1}{n}\sum_{i=1}^nx_i\;$ and $d=2r.\;$ Then $x_{k+1-i}=x-(2i-1)r\;$ and $x_{k+i}=x+(2i-1)r,\;$ $1\le i\le k.\;$ We have
$\displaystyle\begin{align} 1 &= \sum_{i=1}^{n}x_i^2\\ &= \sum_{i=1}^{k}[x-(2i-1)r]^2+\sum_{i=1}^{k}[x+(2i-1)r]^2\\ &=2kx^2+2r^2\sum_{i=1}^{k}(2i-1)^2\\ &=2kx^2+2r^2\frac{k(4k^2-1)}{3}\\ &= nx^2+d^2\frac{(n^2-1)n}{12} \end{align}$
from which $\displaystyle d=\sqrt{\frac{12}{(n^2-1)n}(1-nx^2).}\;$ The maximum $d$ is obtained for $x=0:$
$\displaystyle d=\sqrt{\frac{12}{(n^2-1)n}}.$
Then
$\displaystyle x_1=-\frac{n-1}{2}\sqrt{\frac{12}{(n^2-1)n}}=-\sqrt{\frac{3(n-1)}{n(n+1)}}.$
The same as in the first case!.
Solution 2
Set $x=x_1.\;$ Then
$\displaystyle\begin{align} 1 &= \sum_{i=1}^{n}x_i^2\\ &= \sum_{i=0}^{n-1}(x+di)^2\\ &=nx^2+2xd\sum_{i=0}^{n-1}i+d^2\sum_{i=0}^{n-1}i^2\\ &=nx^2+xdn(n-1)+d^2\frac{(n-1)n(2n-1)}{6}\\ &=n\left[x+\frac{d(n-1)}{2}\right]^2-n\frac{d^2(n-1)^2}{4}+d^2\frac{(n-1)n(2n-1)}{6}\\ &= n\left[x+\frac{d(n-1)}{2}\right]^2+d^2\frac{(n^2-1)n}{12}. \end{align}$
$d^2\;$ is maximal when the squared bracket is $0.$
Acknowledgment
Leo Giugiuc has kindly communicated to me, along with his solution (Solution 1), a problem by Arcady Alt that appeared previously in the Crux Mathematicorum. Solution 2 is by Grégoire Nicollier.
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73555002
