Two Problems by Kunihiko Chikaya
Problem 1
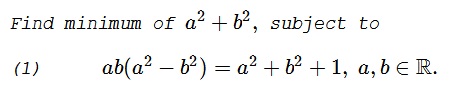
Problem 2
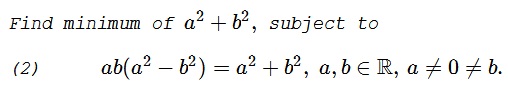
Solution 1 to Problem 1
Either $a=0$ or $b=0$ leads to a contradiction. In any event $a^2+b^2\gt 0.$ It follows that (1) is equivalent to
$\displaystyle \frac{1}{(a^2+b^2)^2}+ \frac{1}{a^2+b^2}=\frac{1}{2}\cdot\frac{2ab}{a^2+b^2}\cdot\frac{a^2-b^2}{a^2+b^2}.$
Now
$\displaystyle \frac{1}{2}\cdot\frac{2ab}{a^2+b^2}\cdot\frac{a^2-b^2}{a^2+b^2}\le\frac{1}{4}\left[\left(\frac{2ab}{a^2+b^2}\right)^2+\left(\frac{a^2-b^2}{a^2+b^2}\right)^2\right]=\frac{1}{4}$
so that
$\displaystyle \frac{1}{(a^2+b^2)^2}+ \frac{1}{a^2+b^2}=\left(\frac{1}{a^2+b^2}+\frac{1}{2}\right)^2\le\frac{1}{2}$
so that
$\displaystyle 0\lt\frac{1}{a^2+b^2}\le\frac{\sqrt{2}-1}{2}.$
Finally, $a^2+b^2\ge 2(1+\sqrt{2}).$
Solution 2 to Problem 1
Let $a=r\cos\phi$ and $b=r\sin\phi$. $a^2+b^2=r^2$. Let $\xi=r^2$.
$\displaystyle ab(a^2-b^2)=a^2+b^2+1 \Rightarrow \sin 4\phi =\frac{4}{\xi^2}+\frac{4}{\xi}.$
Minimum value of $\xi$ corresponds to maximum value of $\sin 4\phi$ that allows for a real $\xi$. This corresponds to $\sin 4\phi=1$ resulting in $\xi^2-4\xi+4=0$ with a positive root of $\xi=2(1+\sqrt{2})$.
Solution 1 to Problem 2
Since $a\ne 0\ne b, $ $a^2+b^2\gt 0,$ making (2) equivalent to
$\displaystyle \frac{2ab}{a^2+b^2}\cdot\frac{a^2-b^2}{a^2+b^2}=\frac{2}{a^2+b^2}.$
Note that $\displaystyle \left(\frac{2ab}{a^2+b^2}\right)^2+\left(\frac{a^2-b^2}{a^2+b^2}\right)^2=1.$
Thus we can set $\displaystyle\frac{2ab}{a^2+b^2}=\cos\theta$ and $\displaystyle\frac{a^2-b^2}{a^2+b^2}=\sin\theta,$ so that (2) becomes $\displaystyle \cos\theta\cdot\sin\theta=\frac{2}{a^2+b^2},$ or $\displaystyle a^2+b^2=\frac{4}{\sin 2\theta}\ge 4,$ with equality for $\sin 2\theta=1.$
Solution 2 to Problem 2
Let $a=r\cos\phi$ and $b=r\sin\phi$. $a^2+b^2=r^2$. Let $\xi=r^2$.
$\displaystyle \begin{align} ab(a^2-b^2)-(a^2+b^2)&=r^4\cos\phi\sin\phi(\cos^2\phi-\sin^2\phi)-r^2 \\ &=\frac{r^4}{2}\sin 2\phi\cos 2\phi -r^2=\frac{\xi^2}{4}\sin 4\phi-\xi. \end{align}$
Hence,
$\displaystyle ab(a^2-b^2)=a^2+b^2 \Rightarrow \xi=\frac{4}{\sin 4\phi}.~(\xi\neq 0).$
Noting that $\xi$ has to be positive, the minimum value of $4$ occurs when $\sin 4\phi=1$.
Acknowledgment
The problems, along with their solutions, were kindly communicated to me by Kunihiko Chikaya. Problem 1 is a recent invention of Bel Jad; Problem 2 was offerred at the 2006 British Mathematical Olympiad (Problem 1). I am grateful to Leo Giugiuc for providing that information. The second solutions are by Amit Itagi.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73608614
