Optimization in a Crooked Trapezoid
Figure ABVU consists of three straight line segments and a circular arc. AU||BV, AU⊥AB. Lines tangent to the arc form trapezoids ABDC.
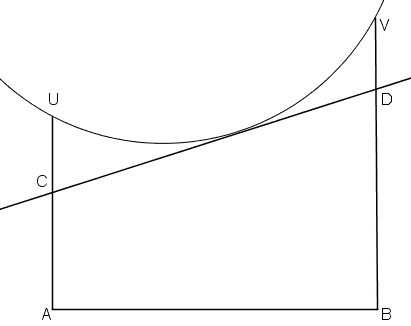
Find the tangent that maximizes the area of ABDC.
|Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander BogomolnyFigure ABVU consists of three straight line segments and a circular arc. AU||BV, AU⊥AB. Lines tangent to the arc form trapezoids ABDC.
Find the tangent that maximizes the area of ABDC.
The area of any trapezoid ABDC can be found from AB×(AC + BD)/2. In this formula an factor (AB) - the height of the trapezoid - is fixed. The problem then is equivalent to maximizing the half-sum of the bases.
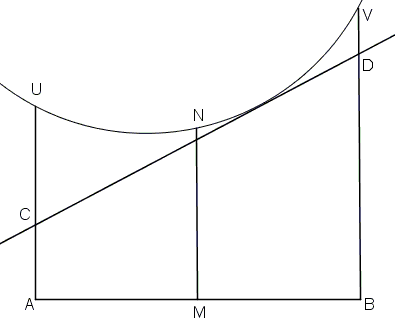
In a trapezoid the half-sum of the bases is equal to the midline - the line parallel to the bases and half way between them. Let M be the midpoint of AB, N on the arc such that MN⊥AB. The tangent at N solves the problem. Indeed, all other tangents cross MN below N so that the corresponding midline is shorter than MN.
Related material
| |
A Sample of Optimization Problems III | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny| 49552170 |
