Angle Trisection By Paper Folding

It is a classical result that, in general, Angle Trisection is impossible by the Euclidean ruler and compass rules. Several methods that went beyond ruler and compass - the neusis constructions - have been known yet to the ancient Greeks (see angle trisection by Archimedes and Hippocrates and a more recent.) Axioms of Paper Folding also supply the tools sufficiently powerful to successfully tackle the angle trisection problem.

The following method of angle trisection is due to H. Abe (1980).

Let's consider an acute angle ABC:
By axiom O4, erect a crease through B perpendicular to AB. (Note that, by O1, AB may be considered a crease.) Execute two creases parallel to AB and at equal distances from each other: BD = DE.
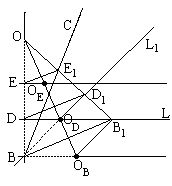
By O6, fold E into BC and B into L. Let B1, D1, E1 be images of points B, D, and E, respectively. Let L1 be the image of crease L. Refold it as to make a crease on the upper part of the paper that remain at rest. Straighten the paper into its original position and fold and unfold crease L1 again. We next show that the crease passes through the point B and, moreover, divides ABC in the ratio 2:1 thus solving the trisection problem.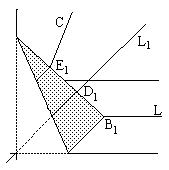
The whole structure is symmetric with respect to the crease OOB. In the isosceles trapezoid BDD1B1, the diagonals intersect on the axis of symmetry. DD1OD is isosceles by construction. Therefore, the creases BD1 and D1OD coincide, or, in other words, D1OD does pass through the vertex B. Now, everything is pretty much straightforward. Just recollect that the crease L is the line DB1 and BOB lies along the given line AB and that, by construction L and AB are parallel. Thus we see that B1BOB = DB1B. Since BODB1 is isosceles, ODBB1 = ODB1B. BD1 is perpendicular to OB1 because OB is perpendicular to DB1. Also, E1D1 = D1B1. This shows that E1BB1 is isosceles and, therefore, E1BD1 = D1BB1.

1. G. E. Martin, Geometric Constructions, Springer, 1998

Paper Folding Geometry

• Angle Trisection by Paper Folding
• Angles in Triangle Add to 180^o
• Broken Chord Theorem by Paper Folding
• Dividing a Segment into Equal Parts by Paper Folding
• Egyptian Triangle By Paper Folding
• My Logo
• Paper Folding And Cutting Sangaku
• Parabola by Paper Folding
• Radius of a Circle by Paper Folding
• An Interesting Example of Angle Trisection by Paperfolding