Distance Between Projections
Here are two apparently similar problems. In the very least, both have solutions that stem from the same basic reasoning.
Problem 1
E and F are projections of point D on the hypotenuse of right triangle ABC on legs AC and BC, respectively. Find D for which EF is minimal.
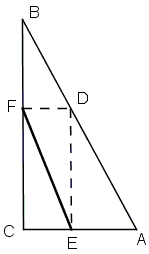
Problem 2
E and F are projections of point D on a quarter circle arc AB on the axes, respectively. Find D for which EF is minimal.
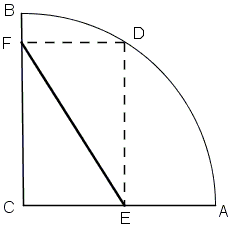
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnySolutions
Problem 1
E and F are projections of point D on the hypotenuse of right triangle ABC on legs AC and BC, respectively. Find D for which EF is minimal.
Draw the second diagonal in rectangle CEDF. Two diagonals in a rectangle are equal. It follows that EF will be shortest whenever CD is. But CD joins vertex C of ΔABC to the opposite side AB. CD is the shortest when it's the altitude from C.
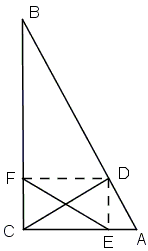
Problem 2
E and F are projections of point D on a quarter circle arc AB on the axes, respectively. Find D for which EF is minimal.
By the same reasoning as in Problem 1, EF is the shortest when the other diagonal CD is. But CD is the radius of the quarter circle and does not depend on theposition of D. The same holds for EF: EF is constant independent of the position of D on the circle.
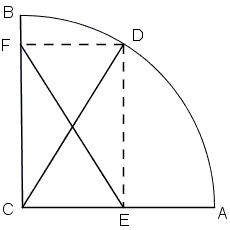
(There is a classical problem by Franciscus van Schooten, related to Problem 2.)
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578455
