Leo Giugiuc's Optimization with Constraint
Problem
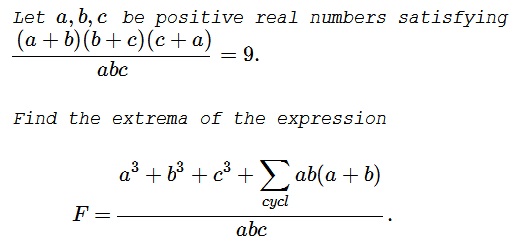
Solution
Let $\displaystyle \frac{b+c}{a}=u,\,\frac{c+a}{b}=v,\,\frac{a+b}{c}=w.\,$ We have $uvw=9\,$ and, since $uvw-(uv+vw+wu)=2,\,$ $u+v+w=9-2=7.\,$ Also,
$\displaystyle q=uv+vw+wu=\frac{\displaystyle a^3+b^3+c^3+\sum_{cycl}ab(a+b)}{abc}+3.$
Consider the function $f:\,(0,\infty)\to\mathbb{R},\,$ defined by $\displaystyle f(x)=\frac{(x-u)(x-v)(x-w)}{x}.\,$ Clearly, $\displaystyle f(x)=x^2-7x-\frac{9}{x}+q,\,$ for $x\ne 0.\,$ Hence, the critical points are $\displaystyle \frac{3}{2}\,$ and $3.$
We form Rolle's sequence: $\displaystyle 0_{+}\lt\frac{3}{2}\lt 3\lt \infty.\,$ Since $f(0_{+})=-\infty,\,$ $f(\infty)=\infty\gt 0\,$ and $f\,$ admits three real roots, by Rolle's theorem, we get $\displaystyle f\left(\frac{3}{2}\right)\ge 0\,$ and $f(3)\le 0,\,$ so that $\displaystyle \frac{57}{4}\le q\le 15.\,$ Moreover, if $\displaystyle u=v=\frac{3}{2}\,$ and $w=4,\,$ $\displaystyle q=\frac{57}{4}\,$ and $uvw=9.\,$ For $u=v=3\,$ and $w=1,\,$ we get $q=15\,$ $uvw=9.$
Now it is easy to find $a,b,c\,$ such that
$\displaystyle\begin{align} &\frac{\displaystyle a^3+b^3+c^3+\sum_{cycl}ab(a+b)}{abc}=\frac{45}{4},\,\text{or,}\\ &\frac{\displaystyle a^3+b^3+c^3+\sum_{cycl}ab(a+b)}{abc}=12. \end{align}$
Acknowledgment
The problem and the solution are due to Leo Giugiuc, who kindly mailed me both.
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73615357
