Regular Octagon by Paper Folding

Paul Yiu starts his exciting paper Elegant Geometric Constructions with a construction of a regular octagon by cutting corners from a square.

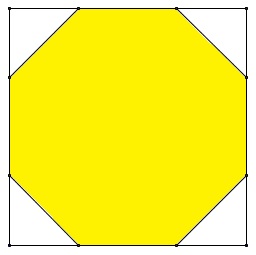
regular octagon in square by cutting corners

When trying to solve this construction, the first impulse is most likely to be looking for the radius of the arcs centered at the vertices of the square that would mark the vertices of the regular octagon:

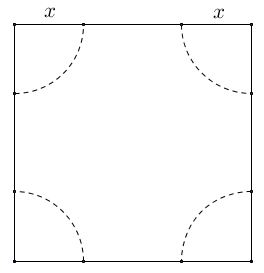
regular octagon in square by cutting corners - first impulse

But on further investigation, a more immediate construction appears to lead to the same result. Assuming, the side of the square is $1$ unit,

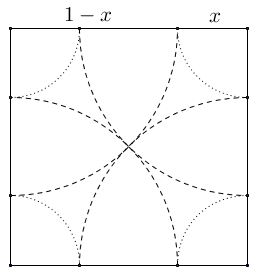
regular octagon in square by cutting corners - construction

The bigger arcs that pass through the center of the square may also be used to determine the vertices of the regular octagon. The computation that validate the claim are straightforward.

For the remaining piece of the side of the unit square to be the side of the regular octagon, we must have the equation $1-2x=\sqrt{2}x:$

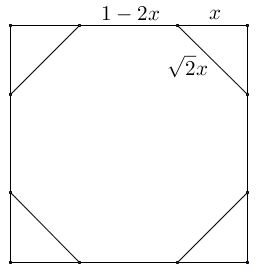
regular octagon in square by cutting corners - explanation

Solving this equation shows that $\displaystyle x=\frac{2-\sqrt{2}}{2},$ implying that $\displaystyle 1-x=\frac{\sqrt{2}}{2},$ exactly half the length of the diagonal of the unit square. This is a pleasant surprise that also suggests an extension to a construction of a regular octagon out of a square by paper folding. Given a square $ABCD$ we proceed in several steps:

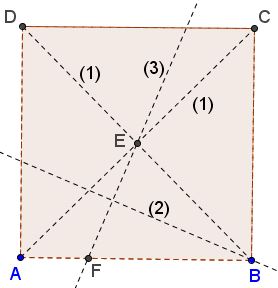
regular octagon by paper folding

Find the center $E$ by folding the two diagonals $AC$ and $BD$ (Axiom O1 or Axiom O2.)
Find the bisector of $\angle ABE$ by folding $BE$ on top of $AB$ (Axiom O3.)
Find point $F$ on $AB$ and the perpendicular to that bisector through $E$ (Axiom O4.)

$F$ is one of the vertices of the regular octagon, because $BF=BE.$ The other seven could be obtained by repeating the above steps or by folding $F$ into the required positions.

Paper Folding Geometry

72111954