Circle Center by Paperfolding
What Is This About?
Problem
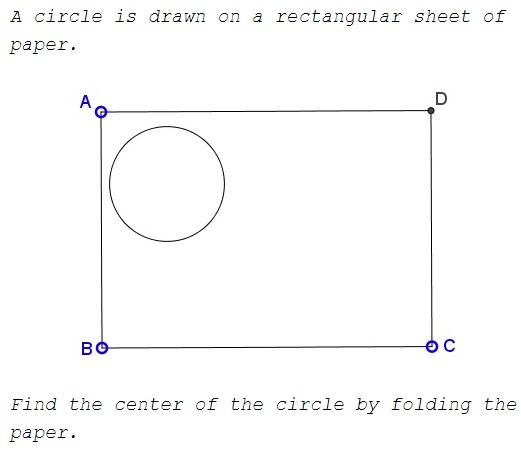
Solution 1
Choose a corner of the sheet and a point on the circle away from the corner. Fold the paper as to place the chosen corner on top of the chosen point $(C'$ and $C$ in the diagram below):
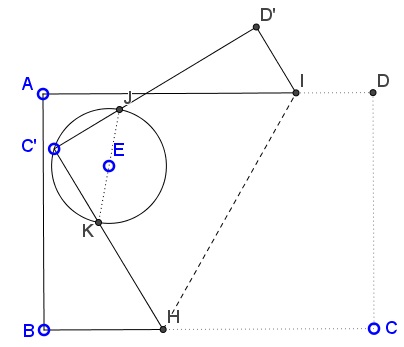
Let the edges of the paper adjacent to $C'$ cross the circle at points $J$ and $K.$ Then, since $\angle JC'K=90^{\circ},$ $JK$ is a diameter of the circle and passes through its center. Make a fold $JK.$
Choose another point on the circle and, perhaps, another corner of the sheet, and repeat the procedure. The two so constructed folds pass both through the center of the circle and, therefore, this is where they cross.
Solution 2
To make sure, I assume that
- You can fold parallel to the sides of the sheet
- Given a point you can fold parallel to one side and passing through that point
- Given two points you can fold through them two
Then:
- Fold parallel to one side in a way that the circle is crossed in 2 points
- From each point fold parallel to the other side. Now you have 2 more points crossing the circle. The 4 points form a rectangle
- Fold the diagonals of the rectangle. They cross at the center
Solution 3
If folding to a tangent is a legitimate operation, fold on three (non parallel) tangents of the circle and then folding on the angel bisectors of the triangle created by the three tangents.
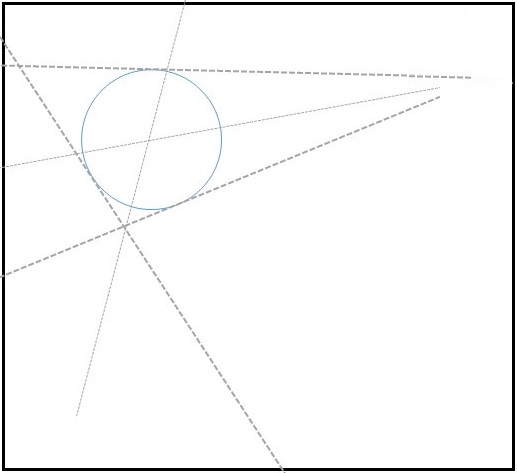
Illustration of a Paperfolding Process

Acknowledgment
This problem was proposed and solved by Thanos Kalogerakis in 2014. Solution 2 is by Luis García; Solution 3 is by Elia Noris. Elia also supplied the illustration.
- An Interesting Example of Angle Trisection by Paperfolding
- Angle Trisection by Paper Folding
- Angles in Triangle Add to 180o
- Broken Chord Theorem by Paper Folding
- Dividing a Segment into Equal Parts by Paper Folding
- Egyptian Triangle By Paper Folding
- Egyptian Triangle By Paper Folding II
- Egyptian Triangle By Paper Folding III
- My Logo
- Paper Folding And Cutting Sangaku
- Parabola by Paper Folding
- Radius of a Circle by Paper Folding
- Regular Pentagon Inscribed in Circle by Paper Folding
- Trigonometry by Paper Folding
- Folding Square in a Line through the Center
- Tangent of 22.5o - Proof Without Words
- Regular Octagon by Paper Folding
- The Shortest Crease
- Fold Square into Equilateral Triangle
- Circle Center by Paperfolding
- Folding and Cutting a Square
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73554751
