A Cyclic Inequality With Constraint in Two Triples of Variables
Problem
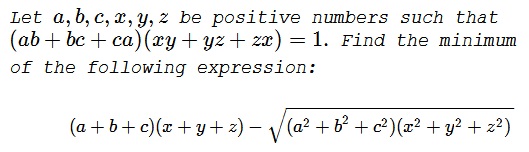
Solution 1
We claim that the requied minimum equals $2.$ Let $a+b+c=3s,$ $x+y+z=3q,$ $ab+bc+ca=3(s^2-t),$ $xy+yz+zx=3(q^2-m),$ with $s,q\gt 0,$ and $0\le t\le s^2,$ $0\le m\le q^2.$ We have $a^2+b^2+c^2=3(s^2+2t)$ and $x^2+y^2+z^2=3(q^2+2m).$ We need to prove that
$3sq-\sqrt{(s^2+2t)(q^2+2m)}\ge 2\sqrt{(s^2-t)(q^2-m)}.$
This is equivalent to
$\begin{align} &\small{9s^2q^2-4(s^2-t)(q^2-m)+(s^2+2t)(q^2+2m)\ge 6sq\sqrt{(s^2+2t)(q^2+2m)}}\;\Rightarrow\\ &s^2q^2+s^2m+q^2t\ge sq\sqrt{(s^2+2t)(q^2+2m)}\;\Rightarrow\\ &(s^2m-q^2t)^2\ge 0, \end{align}$
which is of course true. In order to complete the proof, suffice it to exhibit values of the variables for which equality is attained. This indeed happens, e.g., when $t=m=0,$ i.e., $(a+b+c)^2=3(ab+bc+ca)$ and $(x+y+z)^2=3(xy+yz+zx).$ In other words, the minimum in question is attained when $a^2+b^2+c^2=ab+bc+ca$ and $x^2+y^2+z^2=xy+yz+zx.$ These imply $(a-b)^2+(b-c)^2+(c-a)^=0,$ so that $a=b=c$ and, similarly, $x=y=z.$ For these values the contsraint becomes $9a^2x^2=1,$ i.e., $3ax=1.$ On the other hand, the given expression reduces to $3a\cdot 3x-\sqrt{3a^2\cdot 3x^2}=6ax=2.$
Solution 2
Define $A=a+b+c, D=a^2+b^2+c^2$ and similarly define $A' = x+y+z, D'=x^2+y^2+z^2$. We can then rewrite the constraint as
$(A^2-D)(A'^2-D') = 4.$
Now rewrite the minimization target $f = AA' - \sqrt{DD'} $. We know $A^2 \geq D$ and $A'^2 \geq D'$, so $AA' \geq \sqrt{DD'}$ and thus $f\geq 0$. Instead of minimizing $f$ we can minimize $f^2$ and then take the root:
$\min f = \sqrt{ \min f^2 }.$
But using our constraint:
$\begin{align} f^2 &= A^2A'^2-2AA'\sqrt{DD'}+DD\\ &= 4 + A^2D' + A'^2D - 2AA'\sqrt{DD'}\\ &= 4 + (A\sqrt{D'}-A'\sqrt{D})^2. \end{align}$
$4$ is a lower bound and is reached when $A\sqrt{D'} = A'\sqrt{D}.$ This is surely the case if $A=A',D=D'$, for example
$\displaystyle a=b=c=x=y=z=\frac{1}{\sqrt{3}}.$
Our example fulfills the constraints, so the minimum $4$ of $f^2$ is indeed attained and $\min f = 2.$
Acknowledgment
The problem, with a solution (Solution 1), was kindly communicated to me by Leo Giugiuc. Leo credits the problem to Alijadallah Belabess. Solution 2 is by Long Huynh Huu.
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73562120
