Huygens' Problem
Huygens' problem is superficially similar to that of Heron, but both the methods of solution and the final results are essentially different.
Given a straight line \(\lambda\) and points C and D on the same side from \(\lambda\). Find on \(\lambda\) point \(P\) that minimizes \(CP^{2}+DP^{2}\).
(Just to remind, Heron's problem asked to minimize \(CP+DP\).
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnySolutions
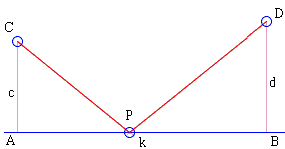
Given a straight line \(\lambda\) and points C and D on the same side from \(\lambda\). \(A\) and \(B\) are projections of points \(C\) and \(D\) on \(\lambda\). Find on \(\lambda\) point \(P\) that minimizes \(CP^{2}+DP^{2}\).

The problem admits an algebraic solution. Define \(A\) and \(B\) as projections of points \(C\) and \(D\) on \(\lambda\). Denote for simplicity \(AC=c\), \(BD=d\), \(AB=k\), and the unknown distance \(AP=x\). According to the Pythagorean theorem or the formula for the Euclidean distance, we are to minimize
\(CP^{2}+DP^{2} = (c^{2}+x^{2})+(d^2+(k-x)^{2})=(c^{2}+d^{2}+k^{2}) + (2x^2-2kx)\).
Introduce function \(f(x)=2x^2-2kx=2x(x-k)\). Since, \(c^{2}+d^{2}+k^{2}\) is a constant for a given configuration, the minimum we are after is attained for the \(x\) that minimizes \(f(x)\).
Function \(f(x)\) is a parabola with the roots at \(0\) and \(k\) so that its axis and the minimum are at \(x=k/2\). Thus, unlike in Heron's problem, the answer does not depend on \(c\) or \(d\).
References
- P. J. Nahin, When Least Is Best, Princeton University Press, 2007 (Fifth printing).
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73561950
