Minimum under Two Constraints
Problem

Solution 1
Clearly, none of $a,b,c\,$ may be zero. Let $ab+bc+ca=s.\,$ Consider the polynomial $P(x)=(x-a)(x-b)(x-c).\,$ Either by Viète's theorem, or carrying out multiplication directly, $P(x)=x^3-x^2\sqrt[3]{3}+sx-\displaystyle \frac{3}{2}.\,$ Now, define the function $\displaystyle f(x)=\frac{P(x)}{x}:\,\mathbb{R}\setminus\{0\}\rightarrow\mathbb{R}.\,$ Obviously, $a,b,c\,$ are the roots of $f(x)=x^2-x\sqrt[3]{3}+s-\displaystyle \frac{3}{2x}.\,$
Further,
$\displaystyle f'(x)=\frac{(2x+\sqrt[3]{3})(2x^2-2x\sqrt[3]{3}+\sqrt[3]{9})}{2x^2},\,$
from which we deduce that $f\,$ is strictly decreasing for $x\le\displaystyle -\frac{\sqrt[3]{3}}{2}\,$ and strictly increasing on $\displaystyle \left[-\frac{\sqrt[3]{3}}{2},0\right)\,$ and on $(0,\infty ).\,$
Since $f(-\infty)=f(0_{-})=\infty,\,$ $f(0_{+})=-\infty,\,$ $f(\infty)=\infty,\,$ it follows that two of $a,b,c\,$ are negative and the third is positive. Let $a,u,v\gt 0,\,$ where $u=-b\,$ and $v=-c.\,$ We have
$\displaystyle \begin{align} (|a|+|b|+|c|)^2 &= a^2+b^2+c^2+2(|ab|+|bc|+|ca|)\\ &=\sqrt[3]{9}-2s+2(au+av+av). \end{align}$
But $s=-au-av+uv,\,$ implying $(|a|+|b|+|c|)^2=\sqrt[3]{9}+4a(a-\sqrt[3]{3}).\,$ On the other hand, $\displaystyle uv=\frac{3}{2a}\,$ and, since $(u+v)^2\ge 4uv,\,$ $\displaystyle (a-\sqrt[3]{3})^2\ge\frac{6}{a}.\,$ From here, $(a-2\sqrt[3]{3})(a^2+\sqrt[3]{9})\ge 0,\,$ so that $a\ge 2\sqrt[3]{3}.\,$ We conclude that $\min (2\sqrt[3]{3}-4a(a-\sqrt[3]{3}))=9\sqrt[3]{9}.$
Hence $\min (|a|+|b|+|c|)=3\sqrt[3]{3}\,$ and is attained at $\displaystyle \left(2\sqrt[3]{3},-\frac{\sqrt[3]{3}}{2},-\frac{\sqrt[3]{3}}{2}\right)\,$ and permutations.
Solution 2
To get the positive product, either all three variables have to be positive or two of the three need to be negative with the third positive. The AM of the three variables is $3^{1/3}/3\,$ and the GM is $3^{1/3}/2^{1/3}.\,$ Thus, the GM being greater than the AM, all three cannot be positive. Without loss in generality, let $b\,$ and $c\,$ be negative. We make a change in variables: $x=a$, $y=-b$, and $z=-c.\,$ Now, all three $\{x,y,z\}\,$ are positive. The constraints become $y+z=x-3^{1/3}\,$ and $yz=3/(2x).\,$ The quantity to minimize is $x+y+z = 2x-3^{1/3}.\,$ The term is monotonically increasing in $x.\,$ The first contraint gives parallel lines in the $YZ\,$ plane that move away from the origin as $x\,$ is increased. The second constraint gives a set of non-intersecting hyperbolas that move towards the origin in the $YZ\,$ plane as $x\,$ is increased. We are interested only in the first quadrant. Note that the tangent to any of the hyperbolas at the point where $y=z\,$ is a line from the family of lines of the first constraint (not necessarily for the same value of $x$). In the extreme case of $x\rightarrow 0$, the line and the hyperbola have no common points. At the other extreme of $x\rightarrow \infty$, the line and the hyperbola have two common points. As $x\,$ is decreased towards $0\,$ from a very large value, the two common points come closer together and for some value of $x\,$ they coalesce into a single point where the line is tangent to the hyperbola. This point has $y=z.\,$ If $x\,$ is further decreased, the contraints have no common point. Thus, the case of tangency corresponds to the minimum of our function.
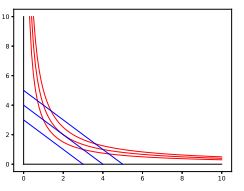
Thus, $2y=x-3^{1/3}\,$ and $y^2=3/(2x).\,$ Eliminating $x,\,$
$\begin{align} y^3+\frac{3^{1/3}}{2}y^2-\frac{3}{4}&=0, \\ \left(y-\frac{3^{1/3}}{2}\right)\left[\left(y+\frac{3^{1/3}}{2}\right)^2+\frac{3^{2/3}}{4}\right]&=0. \end{align}$
There is only one real root at $y=3^{1/3}/2.\,$ Thus, $z=3^{1/3}/2\,$ and $x=2y+3^{1/3}=2\cdot 3^{1/3}.\,$ Thus, $\min (x+y+z) = 3 \cdot 3^{1/3}.$
Acknowledgment
The problem, along with his solution (Solution 1), has been communicated to me by Leo Giugiuc. The problem has been previously posted at the artofproblemsolving forum. Solution 2 is by Amit Itagi.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73574742
