Menelaus Theorem: Proofs Ugly and Elegant
A. Einstein's View
In a discussion on the Menelaus Theorem we presented two proofs: a short one and another that required a little more effort but led to some insights into the interplay between the theorem and other parts of geometry. Not long ago I came across a post An Ugly and an Elegant Proof of Menelaus Theorem by Antreas P. Hatzipolakis at the geom.college newsgroup. The message referred to an article in Math. Intelligencer that commented on correspondence between Albert Einstein and a friend of his, Max Wertheimer. In the first letter, Einstein apparently continues a discussion on elegance of mathematical proofs. A proof may require introduction of additional elements, like line AP in the first of the cited proofs. In Einstein's opinion, "... we are completely satisfied only if we feel of each intermediate concept that it has to do with the proposition to be proved."
As an illustration of his viewpoint, Einstein gives two proofs of the same proposition - one ugly, the other elegant. Curiously, the proposition he proves is that of the Menelaus theorem, and the proof ugly in his view is the first of the cited proofs. He writes, "Although the first proof is somewhat simpler, it is not satisfying. For it uses an auxiliary line which has nothing to do with the content of the proposition to be proved, and the proof favors, for no reason, the vertex A, although the proposition is symmetrical in relation to A, B, and C. The second proof, however, is symmetrical, and can be read off directly from the figure."
| What if applet does not run? |
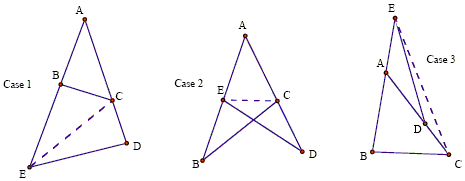
I adapt Einstein's second proof to the notations I used previously. It uses the principle that two triangles with a common (or supplementary) angle are related as the products of adjacent sides. (In the manner of the Ancients, Einstein means here the ratio of the areas of two triangles, and refers to the formula that gives the area as half the product of two sides and the sine of the angle between them.) We choose as these triangles those formed by the individual vertices of the triangle with the corresponding segments of the transversal: ΔAEF, and (those formed derived from it by cyclical transformation) ΔBFD, ΔCDE. We have
| (1) | area( Δ AEF)/area( Δ BFD) = AF·EF / BF·DF. |
If this equation is multiplied by those derived from it by cyclical transformation, we obtain
| (2) | 1 = AF·BD·CE / BF·CD·AE, |
as required.
Elegance, as beauty, is in the eye of the beholder. I agree with Einstein on one point and disagree on another. Line AP appears to be an artificial construct as it destroys the inner symmetry of the theorem. However, I think I mind less using auxiliary constructs. The additional lines in the second of the cited proofs helped relate (and that quite unexpectedly) the Menelaus Theorem to the homothety transformation and its properties. (The 4 travellers problem and one of its proofs serve as another example where a considerable benefit is drawn from an introduction of additional elements. The proof adds a 3-dimensional frame to a 2-dimensional problem making the whole picture a work of art.)
Yet another proof [F. G.-M., p. 84] adds elements to the original diagram. Like Proof #2 it does so in a symmetric manner. It renders the theorem virtually trivial.
Draw a line perpendicular to the transversal EDF. Let it intersect the latter at point K, and denote the projections of the vertices A, B, C on that line as Ka, Kb, and Kc, respectively. As is well known, the segments cut on two lines by a family of parallel lines are in the same ratio. Pairing the side lines of ΔABC with the just constructed lines one at a time we get:
| AF/BF = KaK/KbK, BD/CD = KbK/KcK, CE/AE = KcK/KaK, |
so that obviously
| AF/BF · BD/CD · CE/AE = KaK/KbK · KbK/KcK · KcK/KaK = 1. |
Ram Tobolski has observed that the extra line need not be perpendicular to the transversal. Suffice it to draw three parallels to the transversal through the vertices of the triangle and then any line that meets them all.
Einstein's proof employs in (1) the sine formula for the area of a triangle. Dependence on a trigonometric function makes an otherwise simple proof unsuitable to students in the first year geometry. This point was brought to me by Charles Worrall, a high school teacher at Horace Mann School in New York City. In his class, Menelaus' and Ceva's theorem came even before a discussion on similarity that might have obviated the need in the sine function. Nonetheless, Charles found the following workaround that leads to (1) eschewing both triginometry and similarity.
Charles came up with the following
Lemma
|
Let (XYZ) denote the area of triangle XYZ. Then, with a reference to the diagram above,
|
Proof
Because pairs of triangles share an altitude,
| and |
|
Multiplying the two completes the proof.
Lemma allows to obtain all three identities whose product (after some cancellations) leads to (2).
References
- Abraham S. Luchins; Edith H. Luchins: The Einstein-Wertheimer Correspondence on Geometric Proofs and Mathematical Puzzles. Math. Intelligencer 12, No.2, 35-43 (1990).
- F. G.-M., Exercices de Géométrie, Éditions Jacques Gabay, sixiéme édition, 1991
Menelaus and Ceva
- The Menelaus Theorem
- Menelaus Theorem: proofs ugly and elegant - A. Einstein's view
- Ceva's Theorem
- Ceva in Circumscribed Quadrilateral
- Ceva's Theorem: A Matter of Appreciation
- Ceva and Menelaus Meet on the Roads
- Menelaus From Ceva
- Menelaus and Ceva Theorems
- Ceva and Menelaus Theorems for Angle Bisectors
- Ceva's Theorem: Proof Without Words
- Cevian Cradle
- Cevian Cradle II
- Cevian Nest
- Cevian Triangle
- An Application of Ceva's Theorem
- Trigonometric Form of Ceva's Theorem
- Two Proofs of Menelaus Theorem
- Simultaneous Generalization of the Theorems of Ceva and Menelaus
- Menelaus from 3D
- Terquem's Theorem
- Cross Points in a Polygon
- Two Cevians and Proportions in a Triangle, II
- Concurrence Not from School Geometry
- Two Triangles Inscribed in a Conic - with Elementary Solution
- From One Collinearity to Another
- Concurrence in Right Triangle

|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73580462
