Much from Little
Introduction
Below is an adaptation of John Molokach's article that he communicated on Friday, 23 December 2016.
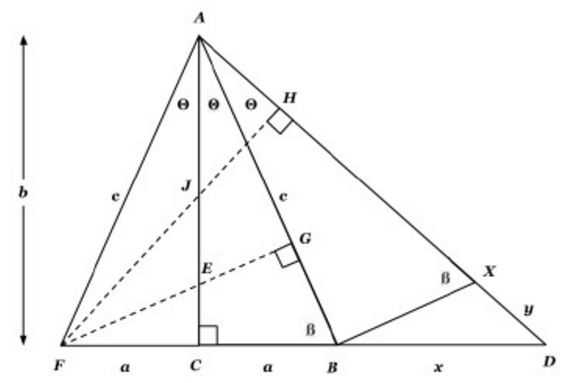
In the diagram above, let $\Delta ABC\,$ be a right triangle with right angles C and legs $a\,$ and $b.\,$ Label the opposite angles from legs $a\,$ and $b,\,$ $\theta\,$ and $\beta,\,$ respectively. Then construct $\Delta BAX\,$ such that $\angle ABX\,$ is right with $\angle BAX=\theta.\,$ Also extend $AX\,$ and $BC\,$ to their intersection $D\,$ to form $\Delta CAD.\,$ Finally, reflect $\Delta ABC \,$ over $AC\,$ to form $\Delta ACF.$
We shall use this diagram to prove:
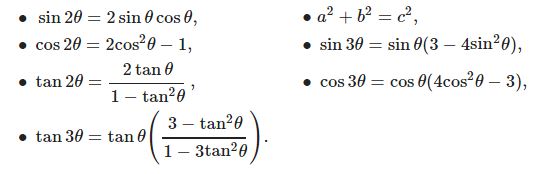
$\sin 2\theta=2\sin\theta\cos\theta$

The area of $\Delta FAB$ is $[\Delta FAB]=ab=\displaystyle\frac{AB\cdot FG}{2}.\,$ Therefore, $FG=\displaystyle\frac{2ab}{c},\,$ i.e.,
$\sin2\theta=\displaystyle\frac{2ab}{c^2}=2\sin\theta\cos\theta.$
$\cos 2\theta=2\cos^2\theta-1$

From the Angle Bisector Theorem, $\displaystyle\frac{AF}{AG}=\frac{EF}{EG}\,$ so that $AF=\displaystyle\frac{AG\cdot EF}{EG}\,$ and $EF+EG=FG.\,$ Since $\displaystyle\frac{EF}{AB}=\frac{CF}{AC}\,$ also $EF=\displaystyle\frac{ac}{b}.\,$ It follows that $EG=\displaystyle\frac{2ab}{c}-\frac{ac}{b}=\frac{2ab^2-ac^2}{bc}.\,$ Now, since $\displaystyle\frac{EG}{a}=\frac{AG}{b},\,$ it follows that $AG=\displaystyle\frac{2b^2-c^2}{c}.\,$ Therefore, $\cos 2\theta=\displaystyle\frac{AG}{c}=\frac{2b^2-c^2}{c^2}=2\cos^2\theta -1.$
$a^2+b^2=c^2$

Note that, since triangles $ACB\,$ and $ABX\,$ are similar, $\displaystyle\frac{AB}{BX}=\frac{b}{a}.\,$ Also, since triangles $ABD\,$ and $BXD\,$ are similar, $\displaystyle\frac{x}{y}=\frac{AB}{BX},\,$ and so $\displaystyle\frac{x}{y}=\frac{b}{a}=\tan\beta.$
Now, again from the similarity of triangles $ABD\,$ and $BXD,\,$ we have $\displaystyle\frac{AD}{BD}=\frac{x}{y}=\frac{b}{a}.\,$ Therefore, $x=\displaystyle\frac{b}{a}\left(\frac{c^2}{b}+y\right)=\frac{b}{a}\left(\frac{c^2}{b}+\frac{ax}{b}\right),\,$ implying $x=\displaystyle\frac{ac^2}{b^2-a^2}.$
But also, since $\sin 2\theta=\displaystyle\frac{2ab}{c^2}=\frac{a+x}{c^2/b+y}=\frac{a+x}{c^2/b+ax/b},\,$ we have $x=\displaystyle\frac{ac^2}{2b^2-c^2}.\,$ Equating the two expressions for $x\,$ yields $2b^2-c^2=b^2-a^2,\,$ i.e., $a^2+b^2=c^2.$
$\displaystyle\tan 2\theta=\frac{2\tan\theta}{1-\tan^2\theta}$

Dividing both sides of $a^2+b^2=c^2\,$ by $a^2\,$ results in $1+\tan^2\theta=\sec^2\theta.\,$ We can use this fact, along with the expressions above for $\sin 2\theta\,$ and $\cos 2\theta\,$ to write an expression for $\tan 2\theta:$
$\displaystyle\tan 2\theta=\frac{\sin 2\theta}{\cos 2\theta}=\frac{2\sin\theta\cos\theta}{2\cos^2\theta-1}.$
Now dividing the numerator and the denumerator of this last expression by $\cos^2\theta,\,$ we can write
$\displaystyle\tan 2\theta=\frac{2\tan\theta}{2-\sec^2\theta}=\frac{2\tan\theta}{1-\tan^2\theta}.$
$\sin 3\theta=\sin\theta (3-4\sin^2\theta)$

Our goal is to find an expression for $\displaystyle\frac{FH}{AF}.\,$ To do so we find the area of $\Delta FAD\,$ in two ways. On one hand, $[\Delta FAD]=\displaystyle\frac{DF\cdot AC}{2}.\,$ On the other hand, $[\Delta FAD]=\displaystyle\frac{FH\cdot AD}{2}.\,$ This allows us to write
$\displaystyle b(2a+x)=FH\left(\frac{c^2}{b}+\frac{ax}{b}\right).$
Solving for $FH\,$ an using $x=\displaystyle\frac{ac^2}{2b^2-c^2},\,$ we have $FH=\displaystyle\frac{3ab^2-a^3}{c^2}.\,$ Therefore,
$\displaystyle\frac{FH}{AF}=\sin 3\theta=\frac{a}{c}\left(\frac{4b^2-c^2}{c^2}\right)=\sin\theta (4\cos^2\theta -1).$
Now we can divide both sides of $a^2+b^2=c^2\,$ by $c^2\,$ to obtain $\sin^2\theta+\cos^2\theta=1\,$ and use this result to write
$\sin^3\theta=\sin\theta\left(4-\sin^2\theta -1\right)=\sin\theta (3-4\sin^2\theta ).$
$\cos 3\theta=\cos\theta (4\cos^2\theta-3)$

Our goal is to find an expression for $\displaystyle\frac{AH}{c}.\,$ To do so we shall use an equivalent expression: $\displaystyle\frac{AD}{c}-\frac{DH}{c}.\,$ Applying the Angle Bisector Theorem to $\Delta ACD,\,$ we have $\displaystyle\frac{AD}{b}=\frac{x}{a},\,$ so that $\displaystyle\frac{AD}{c}=\frac{bx}{ac}.\,$
Also, from $\Delta FHD\,$ and the double argument formula, derived earlier,
$\displaystyle\cos\angle FHD=\sin 2\theta=\frac{DH}{2a+x}=\frac{2ab}{c^2},$
so that
$\displaystyle\frac{DH}{c}=\frac{2ab(2a+x)}{c^3}.$
This gives us an expression for $\cos 3\theta:$
$\displaystyle\begin{align} \cos 3\theta &= \frac{AD}{c}-\frac{DH}{c}=\frac{bx}{ac}-\frac{2ab(2a+x)}{c}\\ &=\frac{b}{c}\left(\frac{x}{a}-\frac{2a(2a+x)}{c}\right)=\frac{b}{c}\left(x\left(\frac{1}{a}-\frac{2a}{c^2}\right)-\frac{4a^2}{c^2}\right)\\ &=\frac{b}{c}\left(x\left(\frac{c^2-2a^2}{ac^2}\right)-\frac{4a^2}{c^2}\right). \end{align}$
Now, using $x=\displaystyle\frac{ac^2}{c^2-2ac^2}\,$ from the previous proof, we have
$\displaystyle\cos 3\theta=\frac{b}{c}\left(1-\frac{4a^2}{c^2}\right)=\cos\theta\left(1-4\sin^2\theta\right),$
and once again using $\cos^2\theta+\sin^2\theta=1,\,$ we arrive at our goal:
$\cos 3\theta=\cos\theta\left(4\cos^2\theta-3\right).$
$\displaystyle\tan 3\theta=\tan\theta\left(\frac{3-\tan^2\theta}{1-3\tan^2\theta}\right)$

Now we want to find an expression for $\displaystyle\frac{FH}{AH}\,$ in terms of $a\,$ and $b.\,$ From the previous proof, we can write
$\displaystyle AH=b\left(1-\frac{4a^2}{c^2}\right)=\frac{b}{c^2}(c^2-4a^2).$
With $a^2+b^2=c^2\,$ this gives
$\displaystyle AH==\frac{b}{c^2}(b^2-3a^2).$
From the previous section, $\displaystyle FH=\frac{a}{c^2}(3b^2-a^2)\,$ such that
$\displaystyle \tan 3\theta=\frac{FH}{AH}=\frac{a}{b}\left(\frac{3b^2-a^2}{b^2-3a^2}\right)$
and dividing the numerator and the denumerator by $b^2\,$ we get
$\displaystyle \tan 3\theta=\frac{FH}{AH}=\tan\theta\left(\frac{3-\tan^2\theta}{1-3\tan^2\theta}\right).$
Trigonometry
- What Is Trigonometry?
- Addition and Subtraction Formulas for Sine and Cosine
- The Law of Cosines (Cosine Rule)
- Cosine of 36 degrees
- Tangent of 22.5o - Proof Wthout Words
- Sine and Cosine of 15 Degrees Angle
- Sine, Cosine, and Ptolemy's Theorem
- arctan(1) + arctan(2) + arctan(3) = π
- Trigonometry by Watching
- arctan(1/2) + arctan(1/3) = arctan(1)
- Morley's Miracle
- Napoleon's Theorem
- A Trigonometric Solution to a Difficult Sangaku Problem
- Trigonometric Form of Complex Numbers
- Derivatives of Sine and Cosine
- ΔABC is right iff sin²A + sin²B + sin²C = 2
- Advanced Identities
- Hunting Right Angles
- Point on Bisector in Right Angle
- Trigonometric Identities with Arctangents
- The Concurrency of the Altitudes in a Triangle - Trigonometric Proof
- Butterfly Trigonometry
- Binet's Formula with Cosines
- Another Face and Proof of a Trigonometric Identity
- cos/sin inequality
- On the Intersection of kx and |sin(x)|
- Cevians And Semicircles
- Double and Half Angle Formulas
- A Nice Trig Formula
- Another Golden Ratio in Semicircle
- Leo Giugiuc's Trigonometric Lemma
- Another Property of Points on Incircle
- Much from Little
- The Law of Cosines and the Law of Sines Are Equivalent
- Wonderful Trigonometry In Equilateral Triangle
- A Trigonometric Observation in Right Triangle
- A Quick Proof of cos(pi/7)cos(2.pi/7)cos(3.pi/7)=1/8
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73579131
