Addition and Subtraction Formulas for Sine and Cosine

In a right triangle with legs a and b and hypotenuse c, and angle α opposite side a, the trigonometric functions sine and cosine are defined as

sinα = a/c, cosα = b/c.

This definition only covers the case of acute positive angles α: 0<α<90°. Thus originally both functions are only defined for those values of α. There are good reasons for extending both functions to other values of the angle, but to do so, even for 0 or 90°, requires additional definitions. Without appropriate extensions, the definitions only permit to derive formulas subject to the angle limitations. For example, directly from the definition,

sin(90° - α) = cosα and cos(90° - α) = sinα,

for 0 < α < 90° because these limitations of α also imply the same limitations on 90°-α: 0 < 90°-α < 90°.

We are concerned here with illustrating two pairs of formulas known as the Sine and Cosine Addition and Subtraction formulas, i.e., the formulas for sin(α±β) and cos(α±β), where all the angles involved satisfy the basic limitations:

	0 < α, β, α + β, < 90°, for addition, and
	0 < α, β, α - β < 90°, for subtraction.

Naturally, after the common extension of the definitions, the formulas remain true for all values of the two angles.

So, given two right triangles, one with angle α and the other with angle β. For the sake of a geometric illustration, we need to put those triangles somehow together to make a combination of angles α and β to stand out. As is suggested in [Gelfand & Saul, p. 126], there are just three ways of doing that:

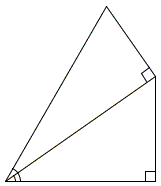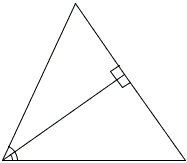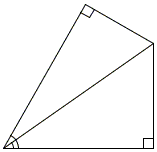The third one is the basis for the derivation of the formulas for sin(α±β). We expand this diagram below to a proof without words for sin(α-β) and cos(α-β) [Zimba] and the first one to illustrate the addition formulas [Gelfand & Saul, pp. 127-128]. The middle one can be used to prove the formula for sin(α+β) via the triangle area formula.

Formulas for sin(α + β) and cos(α + β)

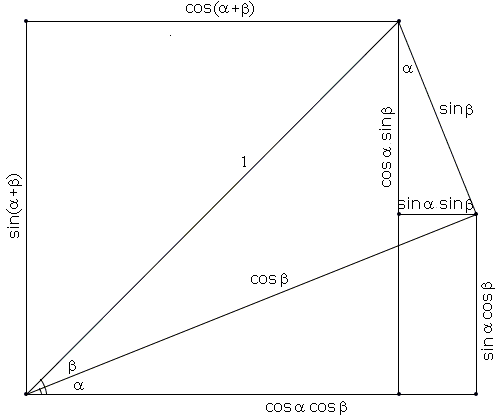
	sin(α + β) = sinα cos β + cos α sin β.
	cos(α + β) = cosα cos β - sin α sin β.

Formulas for sin(α - β) and cos(α - β)

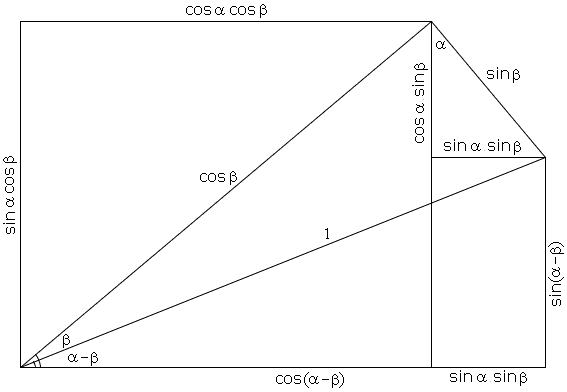
	sin(α - β) = sinα cos β - cos α sin β.
	cos(α - β) = cosα cos β + sin α sin β.

Another Proof of sin(α + β) = sinα cos β + cos α sin β

The next proof relies on the diagram:

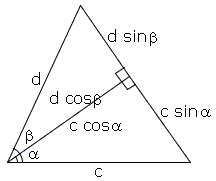
From the definition of sine and the fact that the area of a triangle is half the product of the altitude and the base, it follows that the are of a triangle is half the product of any of the two side times sin of the included angle. For the three triangles in the diagram we have

	2A_c	= c (d cosβ) sinα,
	2A_d	= d (c cosα) sinβ,
	2A	= cd sin(α + β).

Which after cancelling cd gives the addition formula for sine.

Observe that in this proof α + β need not be acute. (This proof alongside a similar one for sin(α - β) - both by S. Kung - appear also in [Nelsen, p. 30]. It was also reproduced in [Nelsen II, p. 39] with attribution to C. Brueningsen. Another set of proofs without words of all four formulas appear on a separate page. The latest modification by J. Molokach has been also placed separately.)

References

I. M. Gelfand, M. Saul, Trigonometry, Birkhäuser, 2001
R. B. Nelsen, Proofs Without Words, MAA, 1993
R. B. Nelsen, Proofs Without Words II, MAA, 2000
J. Zimba, On the Possibility of Trigonometric Proofs of the Pythagorean Theorem, Forum Geometricorum, Volume 9 (2009) 275-278

Trigonometry

72104945