Another Face and Proof of a Trigonometric Identity

Problem 2 at the 2007 Irish Mathematical Olympiad required to prove that the identity $\mbox{sin}^{2}\alpha + \mbox{sin}^{2}\beta +\mbox{sin}^{2}\gamma =2$, where $\alpha +\beta +\gamma = 180^{\circ}$, holds if and only if one of the angles $\alpha$, $\beta$, or $\gamma$ is right. The equivalent identity $\cos ^{2}\alpha + \cos ^{2}\beta +\cos ^{2}\gamma =1$ then appears as a form of the Pythagorean theorem. It came to my attention that in the following reincarnation

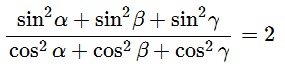
trigonmetric form of the Pythagorean theorem

it was suggested by Poland at the 1967 International Mathematical Olympiad [The IMO Compendium, p. 46].

The equivalence of the three formulations is obvious. Thus, the proof below covers all three.

Assume $\alpha +\beta +\gamma = 180^{\circ}$. Then the identity

$\cos ^{2}\alpha + \cos ^{2}\beta +\cos ^{2}\gamma =1$

Holds if and only if one of the angles $\alpha$, $\beta$, or $\gamma$ is right.

Proof 1

Multiply the identity by 2 and regroup:

$(2\cos ^{2}\alpha -1) + (2\cos ^{2}\beta -1) +2\cos ^{2}\gamma =0$.

By the double argument formulas, $2\cos ^{2}t -1=\cos (2t)$, this is converted to

$\cos 2\alpha + \cos 2\beta +2\cos ^{2}\gamma =0$.

Next apply the edition formulas $\cos (2s)+\cos (2t)=2\cos (s-t)\cos (s+t)$ to obtain

$\cos (\alpha -\beta)\cos (\alpha +\beta) +\cos ^{2}\gamma =0$.

Taking into account that, by the stipulation of the problem, $\cos \gamma = -\cos (\alpha +\beta)$, we factor the latter

$\cos \gamma\space (\cos (\alpha -\beta)-\cos \gamma) =0$.

It follows that either $\cos \gamma =0$ or $\cos (\alpha -\beta) -\cos \gamma =\cos (\alpha -\beta) +\cos (\alpha +\beta) =0$. In the former case, $\gamma$ is right.

In the latter case, $\cos (\alpha -\beta) +\cos (\alpha +\beta)=2\space\cos \alpha\space\cos \beta =0$, implying that either $\alpha$ or $\beta$ is right.

Proof 2

As was suggested by a comment below the expression $\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1\,$ cann be converted into

$(-a^2+b^2+c^2)(a^2-b^2+c^2)(a^2+b^2-c^2)=0\,$

with a required implication. This follows from a known identity

$\cos^2\alpha+\cos^2\beta+\cos^2\gamma+2\cos\alpha\cos\beta\cos\gamma=1\,$

and the Law of Cosines:

$\displaystyle \cos\gamma=\frac{a^2+b^2-c^2}{2ab}, \ldots$

Proof 3

This proof is by mit Itagi.

If the triangle is right, WLOG let $\alpha=90^o$. Thus,

$\displaystyle \begin{align} &\frac{\sin^2 \alpha + \sin^2 \beta + \sin^2 \gamma}{\cos^2 \alpha + \cos^2 \beta + \cos^2 \gamma} \\ &=\frac{1+\sin^2\beta+\sin^2(90^o-\beta)}{\cos^2\beta+\cos^2(90^o-\beta)} \\ &=\frac{1+\sin^2\beta+\cos^2\beta}{\cos^2\beta+\sin^2\beta}=2 \end{align}$

For the converse, let $d$ be the diameter of the circumcircle. Using sine rule,

$\displaystyle \begin{align} &\frac{\sin^2 \alpha + \sin^2 \beta + \sin^2 \gamma}{\cos^2 \alpha + \cos^2 \beta + \cos^2 \gamma}=2 \\ \Rightarrow& \frac{(a^2+b^2+c^2)/d^2}{3-(a^2+b^2+c^2)/d^2}=2 \\ \Rightarrow& (a^2+b^2+c^2)=2d^2 \\ \Rightarrow& (a^2+b^2+c^2)=\frac{a^2+b^2+c^2}{(1+\cos A\cos B\cos C)} \\ \Rightarrow& \cos A\cos B\cos C = 0. \end{align}$

Thus, one of the cosine terms goes to zero and that angle is a right angle.

References

D. Djukic et al, The IMO Compendium, Springer, 2011 (Second edition)

Trigonometry

71940139