A Trigonometric Observation in Right Triangle

Consider a right triangle with the side lengths $a, $ $b,$ $c:$

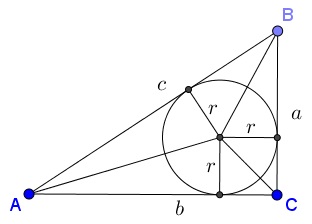
We have:

$\displaystyle\begin{align} \pi&=\arctan\frac{r}{r}+\arctan\frac{a-r}{r}+\arctan\frac{b-r}{r}\\ &=1+\arctan\left(\frac{a}{r}-1\right)+\arctan\left(\frac{b}{r}-1\right)\\ &=1+\arctan\left(\frac{a+b+c}{b}-1\right)+\arctan\left(\frac{a+b+c}{a}-1\right)\;\;\left(\text{for } r=\frac{ab}{a+b+c}\right)\\ &=1+\arctan\frac{a+c}{b}+\arctan\frac{a+c}{a}. \end{align}$

Hence,

$\displaystyle \arctan\left(\frac{b+c}{a}\right)+\arctan\left(\frac{a+c}{b}\right)=\frac{3\pi}{4}.$

On the other hand, it's known that $\displaystyle r=\frac{a+b-c}{2}.$ Thus $\displaystyle a-r=\frac{a-b+c}{2}$ and $\displaystyle b-r=\frac{b-a+c}{2}.$ We conclude that

$\displaystyle\begin{align} \pi&=\arctan\frac{r}{r}+\arctan\frac{a-r}{r}+\arctan\frac{b-r}{r}\\ &=1+\arctan\frac{a-b+c}{a+b-c}+\arctan\frac{b-a+c}{a+b-c}. \end{align}$

From which

$\displaystyle \arctan\left(\frac{a-b+c}{a+b-c}\right)+\arctan\left(\frac{b-a+c}{a+b-c}\right)=\frac{3\pi}{4}.$

More generally, assume $ab,bc,ca\gt 0.$ Since, for $x,y\gt 0,$ $0\lt\arctan x+\arctan y\lt\pi,$

$\displaystyle\begin{align}\tan\left(\arctan\left(\frac{a+c}{b}\right)+\arctan\left(\frac{b+c}{a}\right)\right)&=\frac{\displaystyle \frac{a+c}{b}+\frac{b+c}{a}}{\displaystyle 1-\frac{a+c}{b}\cdot\frac{b+c}{a}}\\ &=-1, \end{align}$

because of $a^2+b^2=c^2.$

We deduce thus that $\displaystyle \frac{\pi}{2}\lt\tan\left(\arctan\left(\frac{a+c}{b}\right)+\arctan\left(\frac{b+c}{a}\right)\right)\lt\pi$ and, since tangent is an injective function on $\displaystyle \left(\frac{\pi}{2},\pi\right),$ then

$\displaystyle \tan\left(\arctan\left(\frac{a+c}{b}\right)+\arctan\left(\frac{b+c}{a}\right)\right)=\tan\frac{3\pi}{4},$

and the conclusion follows.

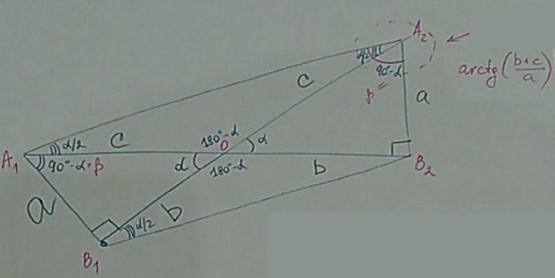
$\angle A_1OB_1=\angle A_2OB_2=\alpha;$ $\angle B_1A_1O=\angle B_2A_2O=90^{\circ}-\alpha.$

In $\Delta A_1OA_2,$ by construction, $A_1O=A_20,$ $\angle A_1OA_2=180^{\circ}-\alpha,$ implying

$\displaystyle \angle OA_1A_2=\angle OA_2A_1=\frac{180^{\circ}-(180^{\circ}-\alpha)}{2}=\frac{\alpha}{2}=\arctan\frac{b+c}{a}.$

Similarly, $\displaystyle \arctan\frac{a+c}{b}=90^{\circ}-\frac{\beta}{2}.$ In conclusion,

$\displaystyle \begin{align} \arctan\frac{b+c}{a}+\arctan\frac{a+c}{b}&=90^{\circ}-\frac{\alpha}{2}+90^{\circ}-\frac{\beta}{2}\\ &=180^{\circ}-\frac{\alpha+\beta}{2}=180^{\circ}-45^{\circ}=135^{\circ}\\ &=\frac{3\pi}{4}. \end{align}$

John Molokach came up with the first formula after watching Trigonometry by Watching. After he informed me of his discovery, in an attempt to prove it, I stumbled on the second expression. Leo Giugiuc gave another (algebraic) proof after observing that the three numbers may as well be negative. Artyom Sedykh gave another purely geometric derivation.