Addition and Subtraction Formulas for Sine and Cosine III
The proofs below of the addition and subtraction formulas for sine and cosine use the least amount of drawing attributes (5 lines each) and combine only three triangles all in an essential way. The proofs are by Leonard M. Smiley, University of Alaska Anchorage. A probably more professional copies of the proofs are available at the MAA site. They have also appeared in [R. Nelsen, pp. 42-43]. Naturally, the proofs are only valid for small angles, the constraints being clear from the diagrams. In fact, all four proofs use exactly same geometric configuration.
Formulas for sin(α - β)
 |
|
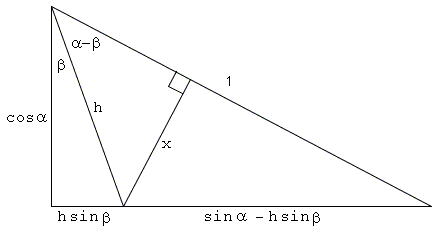| h = cosα / cosβ. x = h sin(α - β). x = (sinα - h sinβ) cosα. | |
| sin(α - β) = sinα cos β - cos α sin β. |
Formulas for cos(α - β)
 | |
| h = cosα / sinβ. x = h cos(α - β). x = (sinα + h cosβ) cosα. | |
| cos(α - β) = cosα cos β + sin α sin β. |
Formulas for cos(α + β)
 | ||||||
| ||||||
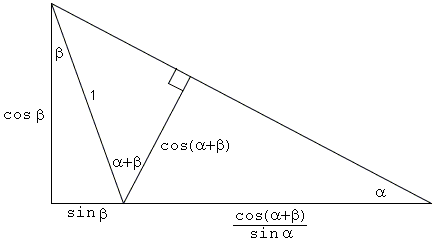| cos(α + β) = cosα cos β - sin α sin β. |
Formulas for sin(α + β)
| ||||||
| ||||||
| sin(α + β) = sinα cos β + cos α sin β. |
References
- R. B. Nelsen, Proofs Without Words II, MAA, 2000
Trigonometry
- What Is Trigonometry?
- Addition and Subtraction Formulas for Sine and Cosine
- Sine of a Sum Formula
- Addition and Subtraction Formulas for Sine and Cosine II
- Addition and Subtraction Formulas for Sine and Cosine III
- Addition and Subtraction Formulas for Sine and Cosine IV
- Addition and Subtraction Formulas
- The Law of Cosines (Cosine Rule)
- Cosine of 36 degrees
- Tangent of 22.5o - Proof Wthout Words
- Sine and Cosine of 15 Degrees Angle
- Sine, Cosine, and Ptolemy's Theorem
- arctan(1) + arctan(2) + arctan(3) = π
- Trigonometry by Watching
- arctan(1/2) + arctan(1/3) = arctan(1)
- Morley's Miracle
- Napoleon's Theorem
- A Trigonometric Solution to a Difficult Sangaku Problem
- Trigonometric Form of Complex Numbers
- Derivatives of Sine and Cosine
- ΔABC is right iff sin²A + sin²B + sin²C = 2
- Advanced Identities
- Hunting Right Angles
- Point on Bisector in Right Angle
- Trigonometric Identities with Arctangents
- The Concurrency of the Altitudes in a Triangle - Trigonometric Proof
- Butterfly Trigonometry
- Binet's Formula with Cosines
- Another Face and Proof of a Trigonometric Identity
- cos/sin inequality
- On the Intersection of kx and |sin(x)|
- Cevians And Semicircles
- Double and Half Angle Formulas
- A Nice Trig Formula
- Another Golden Ratio in Semicircle
- Leo Giugiuc's Trigonometric Lemma
- Another Property of Points on Incircle
- Much from Little
- The Law of Cosines and the Law of Sines Are Equivalent
- Wonderful Trigonometry In Equilateral Triangle
- A Trigonometric Observation in Right Triangle
- A Quick Proof of cos(pi/7)cos(2.pi/7)cos(3.pi/7)=1/8
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny72083946