Sine and Cosine of 15 Degrees Angle

The purpose of this page is to find in closed form values of sine and cosine of the $15^\circ$ angle. Our investigation will be based on the following diagram, which [R. Vakil, p. 97] attributes to Larry Hoehn:

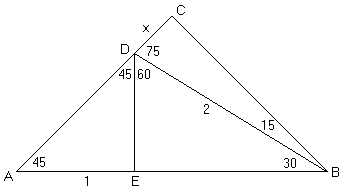
We can place side by side the right isosceles triangle $ADE$ and the $30-60-90$ triangle $BDE$ and then extend $AD$ to $C$ to form another $45-45-90$ triangle $ABC.$ For convenience, we assume that $AE = 1.$ In $\Delta BCD,$ $\angle CBD = 15^\circ.$ This is the triangle whose sides we are hunting.

In $\Delta ADE,$ $DE = 1$ and, by the Pythagorean theorem, $AD = \sqrt{2}.$

In $\Delta BDE,$ $DE = 1$ and $\angle DBE = 30^\circ$ so that $BD = 2$ and $BE=\sqrt{3}.$

In $\Delta ABC,$ $AB = 1 + \sqrt{3}$ so that $AC = BC = (1 + \sqrt{3}) / \sqrt{2}:$

$\displaystyle AC = BC = \frac{\sqrt{2}+\sqrt{6}}{2}.$

Letting $CD=x,$ $AC=\sqrt{2}+x,$ which gives

$\begin{align}\displaystyle x &= \frac{(\sqrt{2}+\sqrt{6})}{2}-\sqrt{2}\\ &=\frac{\sqrt{6}-\sqrt{2}}{2}. \end{align}$

Since $\sin 15^\circ = CD/BD = x/2,$ it follows that

$\displaystyle \sin 15^\circ = \frac{\sqrt{6} - \sqrt{2}}{4}.$

Next, from $BC = (\sqrt{2} + \sqrt{6}) / 2$ and $\cos 15\circ = BC/BD:$

$\displaystyle \cos 15^\circ = \frac{\sqrt{6} + \sqrt{2}}{4}.$

It is reassuring that the values for the sine and cosine of $15^\circ$ fit into the double argument formula $\sin 2\alpha = 2 \sin\alpha\cos\alpha:$

$\displaystyle \begin{align} 2\sin 15^\circ cos 15^\circ &= [(\sqrt{6} - \sqrt{2}) / 4] \times [(\sqrt{6} + \sqrt{2}) / 4]\\ &= 2 (6 - 2) / 16 \\ &= 1 / 2 \\ &= \sin 30^\circ. \end{align}$

For the record, we can also deliver the tangent:

$\tan 15^\circ = 2 - \sqrt{3}.$

Here's another diagram that also offers a way of finding the values of trigonometric function for $15^\circ:$

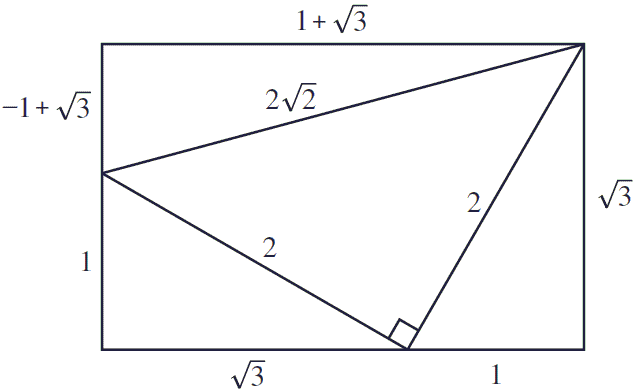
Ailles' rectangle

The values of the trigonometric functions provide a way of establishing that $\angle CBE$ in the diagram below is $15^\circ.$

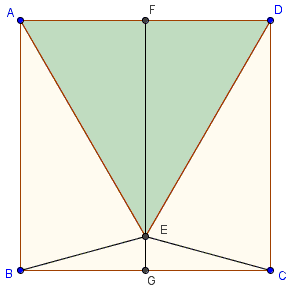
Equilateral triangle in a square and 15 degrees angle

Here $ABCD$ is a square and $ADE$ an equilateral triangle. Indeed, assuming the side of the square equals $1,$ the altitude $EF$ of $\Delta ADE$ is found to be $\displaystyle\frac{\sqrt{3}}{2},$ from which $\displaystyle EG=1-\frac{\sqrt{3}}{2},$ making

$\displaystyle\tan GBE=\frac{EG}{BG}=\frac{1-\sqrt{3}/{2}}{1/2}=2-\sqrt{3}=\tan 15^\circ,$

as we just saw. It follows that $\angle CBE=15^\circ.$

We could have found that without recourse to trigonometry: $AE=AD=AB,$ which makes $\Delta ABE$ isosceles. Its apex

$\angle BAE=\angle BAD-\angle EAD = 90^\circ-60^\circ=30^\circ,$

making its base $\angle ABE=(180^\circ-30^\circ)/2=75^\circ.$ Its complementary $\angle CBE=15^\circ.$ Thus we would have an additional venue for finding the values of the trigonometric functions of $15^\circ.$

Reference

D. S. Ailles, Triangles and trigonometry, Mathematics Teacher 64 (1971) 562
R. Vakil, A Mathematical Mosaic, Brendan Kelly Publishing, 2008 (Expanded Edition)

Trigonometry

71871312