Napoleon's Theorem, Two Simple Proofs

On each side of a triangle, erect an equilateral triangle, lying exterior to the original triangle. Then the segments connecting the centroids of the three equilateral triangles themselves form an equilateral triangle.

By Dr. Scott Brodie, M.D., Ph.D.
Mount Sinai School of Medicine, NY

Proof #1 ("Hammer and Tongs" trigonometry)

In the following, we use standard notations: in the ΔABC, A denotes both the vertex A and the correposnding ∠A, a is both BC and its length. In addition, let G denote the centroid of the equilateral triangle on side AB, and I denote the centroid of the equilateral triangle on side AC, etc. Let s denote the length of segment GI, t the length of segment AG, and u the length of segment AI. (Geometer's SketchPad illustration.)

Since ∠IAC = ∠GAB=30°, we may apply the Law of Cosines to compute

s²= u² + t² - 2ut·cos(A + 60°).

(1)

Since the centroid of a triangle lies along each median, 2/3 of the distance from the vertex to the midpoint of the opposite side, we have

t = (2/3)·sqrt(3)/2 · c = c/sqrt(3)
u = (2/3)·sqrt(3)/2 · b = b/sqrt(3),

and (1) becomes

3·s² = b² + c² - 2bc·cos(A + 60°).

(2)

Expanding^(*) the cosine of the sum, and recalling that cos(60°) = 1/2; sin(60°) = sqrt(3)/2, we have

cos(A + 60°) = cos(A)/2 - sin(A)·sqrt(3)/2.

(3)

Substituting (3) into (2) yields

3·s² = b² + c² - bc·cos(A) + sqrt(3)·bc·sin(A).

(4)

Now apply the Law of Cosines to ΔABC:

a² = b² + c² - 2bc·cos(A).

(5)

and recall (as in the derivation of the Law of Sines):

2·Area( ΔABC) = bc·sin(A).

(6)

Substituting (5) and (6) into (4) gives

3·s² = (1/2)(a² + b² + c²) + 2·sqrt(3)· Area( ΔABC).

(7)

Since (7) is symmetrical in a, b, and c, it follows that the triangle connecting the three centroids is equilateral, QED.

(*)

Michael Lambrou has suggested a different way to proceed after obtaining (2).

Apply the Law of Cosines to triangles ABE and BCE to express the side BE in two different ways:

b² + c² - 2bc·cos(A + 60°) = a² + b² - 2ab·cos(C + 60°)

By (2), the left hand side equals 3 times GI. Similarly, the right hand side equals 3 times IH, wherefrom GI = IH. Considering triangles ACD and ABD instead, we also obtain IH = HG, which furnishes the proof.

As a bonus, we get AD = BE = CF.

Proof #2 (an argument by symmetrization)

Notations are the same as before: let ABC be the original triangle. Choose D, E, and F exterior to ΔABC so that ADB, BEC, and AFC are equilateral triangles, with centroids G, H, and I, respectively. (Geometer's SketchPad illustration.) We proceed to show that ∠HIG = 60°.

Fix I as a center of rotation, and rotate the entire figure by 120°, and superimpose the rotated copy on the original figure. Under the rotation, the ΔCAF maps to itself (C maps to A, A to F, F to C, while I maps into itself.) Denote by BB, DD, EE, GG, and HH the images of points B, D, E, G, and H, respectively.

Connect D to EE and G to HH. By the rigidity of the rotation, ΔGHI = ΔGG.HH.I. In particular, GH = GG.HH. (Geometer's SketchPad illustration.)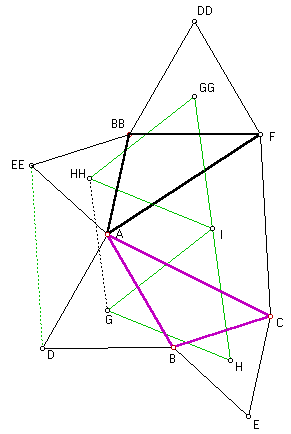

Now consider the six triangles that converge on point A. Three of them (ABD, ACF, and A.EE.BB) are equilateral. Recollect that the angles of a triangle sum to 180°, while the angles around a point sum to 360°. Since ∠BB.A.F is a copy of ∠BCA, it follows that ∠D.A.EE = ∠ABC. Finally, ΔD.A.EE = ΔABC, and the pentagon A.BB.EE.D.B is congruent to the pentagon BECAD. It follows that G.HH = GH. And thus G.HH = GH = GG.HH.

Repeating the rotation by 120° once more, and connecting the tips of the equilateral triangles as above, we obtain the figure on the right. (Geometer's SketchPad illustration.) Arguing as above, it is clear that the central hexagon is equilateral, and that the six triangles which meet at the center of rotation are congruent. Therefore, 6·∠HIG = 360°, and ∠HIG = 60°. Since (among the points G,H,I) the choice of the centroid I was arbitrary, we have shown that ΔGHI is equiangular, hence equilateral, QED.

Napoleon's Theorem

71878569